Feature Space Saturation during Training

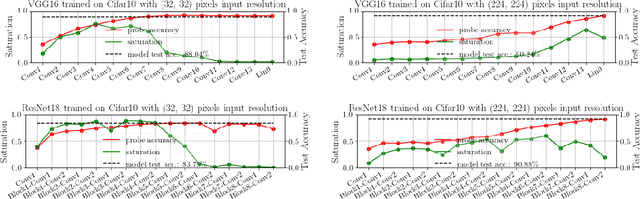
We propose layer saturation - a simple, online-computable method for analyzing the information processing in neural networks. First, we show that a layer's output can be restricted to the eigenspace of its variance matrix without performance loss. We propose a computationally lightweight method for approximating the variance matrix during training. From the dimension of its lossless eigenspace we derive layer saturation - the ratio between the eigenspace dimension and layer width. We show that saturation seems to indicate which layers contribute to network performance. We demonstrate how to alter layer saturation in a neural network by changing network depth, filter sizes and input resolution. Furthermore, we show that well-chosen input resolution increases network performance by distributing the inference process more evenly across the network.

Spectral Analysis of Latent Representations

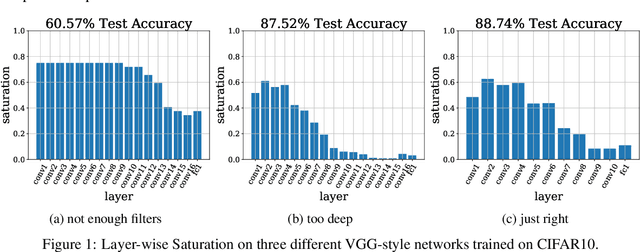
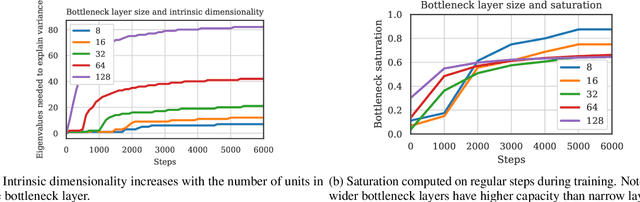
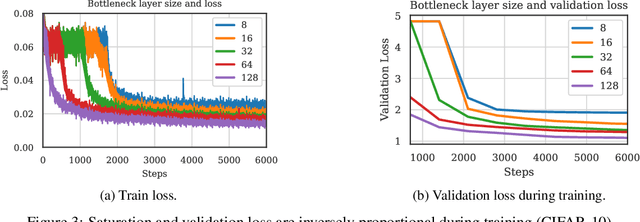
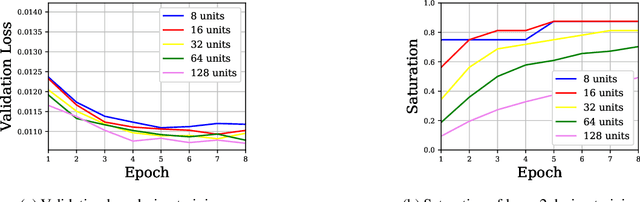
We propose a metric, Layer Saturation, defined as the proportion of the number of eigenvalues needed to explain 99% of the variance of the latent representations, for analyzing the learned representations of neural network layers. Saturation is based on spectral analysis and can be computed efficiently, making live analysis of the representations practical during training. We provide an outlook for future applications of this metric by outlining the behaviour of layer saturation in different neural architectures and problems. We further show that saturation is related to the generalization and predictive performance of neural networks.