Michalkiewicz Mateusz
Implicitly Defined Layers in Neural Networks
Mar 03, 2020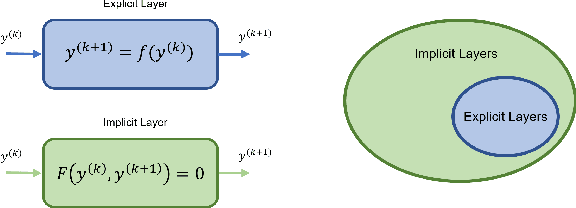

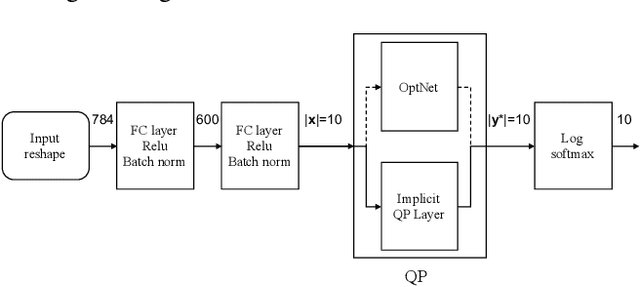
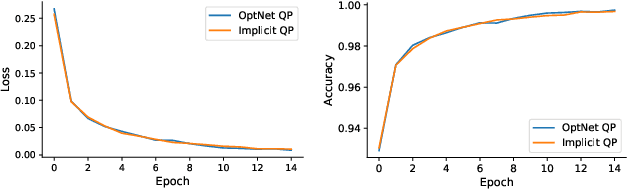
Abstract:In conventional formulations of multilayer feedforward neural networks, the individual layers are customarily defined by explicit functions. In this paper we demonstrate that defining individual layers in a neural network \emph{implicitly} provide much richer representations over the standard explicit one, consequently enabling a vastly broader class of end-to-end trainable architectures. We present a general framework of implicitly defined layers, where much of the theoretical analysis of such layers can be addressed through the implicit function theorem. We also show how implicitly defined layers can be seamlessly incorporated into existing machine learning libraries. In particular with respect to current automatic differentiation techniques for use in backpropagation based training. Finally, we demonstrate the versatility and relevance of our proposed approach on a number of diverse example problems with promising results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge