The FEDHC Bayesian network learning algorithm

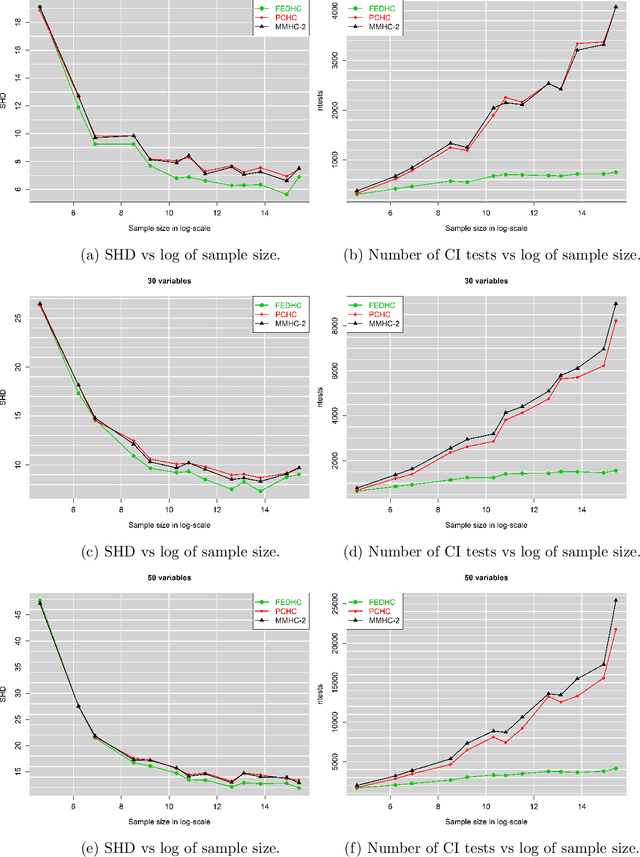
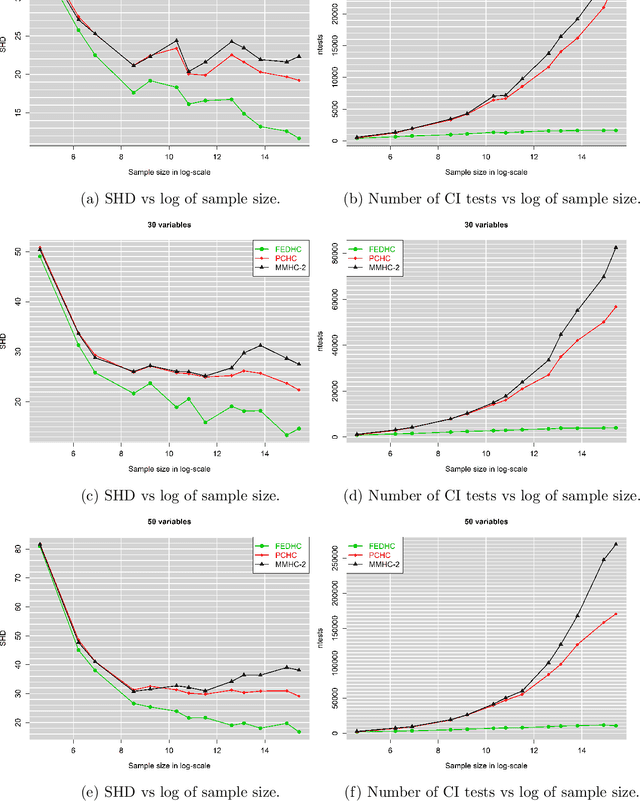
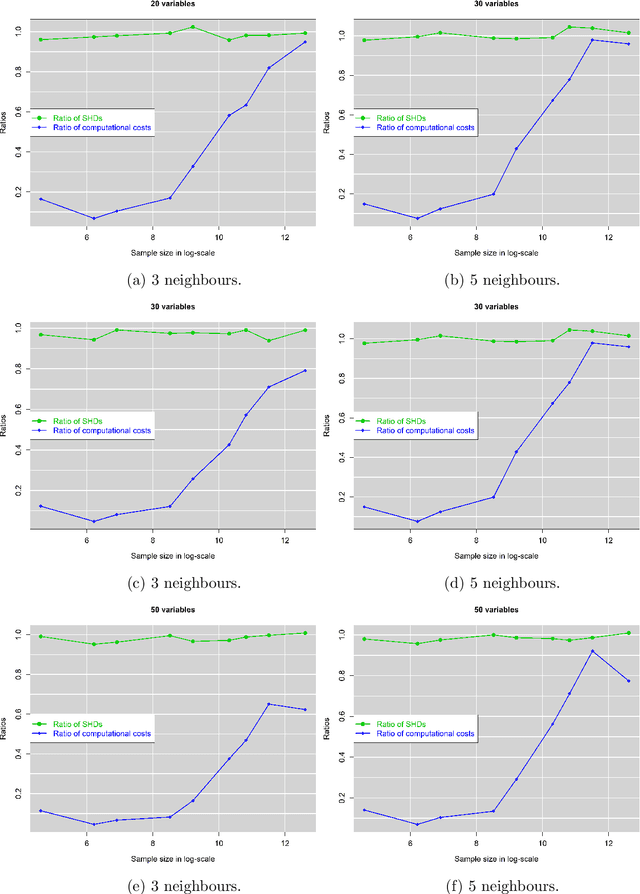
The paper proposes a new hybrid Bayesian network learning algorithm, termed Forward Early Dropping Hill Climbing (FEDHC), designed to work with either continuous or categorical data. FEDHC consists of a skeleton identification phase (learning the conditional associations among the variables) followed by the scoring phase that assigns the causal directions. Specifically for the case of continuous data, a robust to outliers version of FEDHC is also proposed. The paper manifests that the only implementation of MMHC in the statistical software \textit{R}, is prohibitively expensive and a new implementation is offered. The FEDHC is tested via Monte Carlo simulations that distinctly show it is computationally efficient, and produces Bayesian networks of similar to, or of higher accuracy than MMHC and PCHC. FEDHC yields more accurate Bayesian networks than PCHC with continuous data but less accurate with categorical data. Finally, an application of FEDHC, PCHC and MMHC algorithms to real data, from the field of economics, is demonstrated using the statistical software \textit{R}.

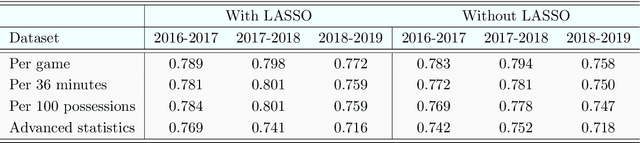
Are NBA players getting paid according to their performance on court?

It is customary for researchers and practitioners to fit linear models in order to predict NBA player's salary based on the players' performance on court. However, in reality the behaviour of the association is non-linear and in this article we take this into account. We first select the most important determinants or statistics (years of experience in the league, games played, etc.) using the LASSO penalised regression and then utilise those determinants to predict the player salaries by employing the non linear Random Forest algorithm. We externally evaluate our salary predictions, via cross-validation, thus we avoid the phenomenon of over-fitting observed in most papers. Overall, using data from three distinct periods, 2017-2019 we identify the important factors that achieve very satisfactory salary predictions and we draw useful conclusions.

A generalised OMP algorithm for feature selection with application to gene expression data

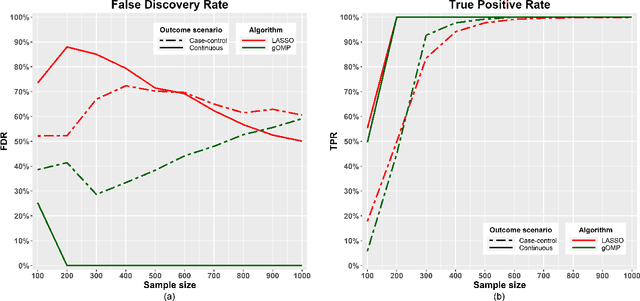
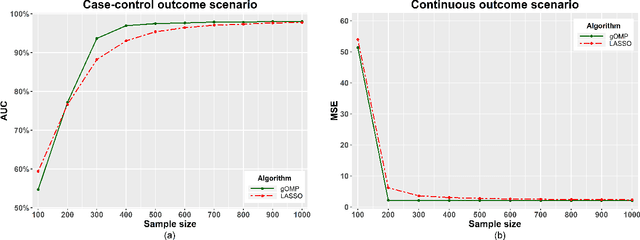
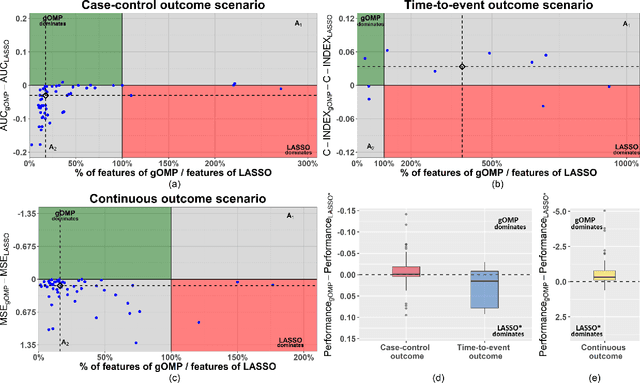
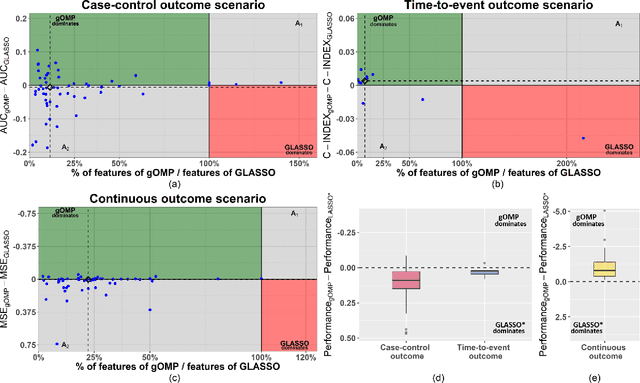
Feature selection for predictive analytics is the problem of identifying a minimal-size subset of features that is maximally predictive of an outcome of interest. To apply to molecular data, feature selection algorithms need to be scalable to tens of thousands of available features. In this paper, we propose gOMP, a highly-scalable generalisation of the Orthogonal Matching Pursuit feature selection algorithm to several directions: (a) different types of outcomes, such as continuous, binary, nominal, and time-to-event, (b) different types of predictive models (e.g., linear least squares, logistic regression), (c) different types of predictive features (continuous, categorical), and (d) different, statistical-based stopping criteria. We compare the proposed algorithm against LASSO, a prototypical, widely used algorithm for high-dimensional data. On dozens of simulated datasets, as well as, real gene expression datasets, gOMP is on par, or outperforms LASSO for case-control binary classification, quantified outcomes (regression), and (censored) survival times (time-to-event) analysis. gOMP has also several theoretical advantages that are discussed. While gOMP is based on quite simple and basic statistical ideas, easy to implement and to generalize, we also show in an extensive evaluation that it is also quite effective in bioinformatics analysis settings.

A folded model for compositional data analysis

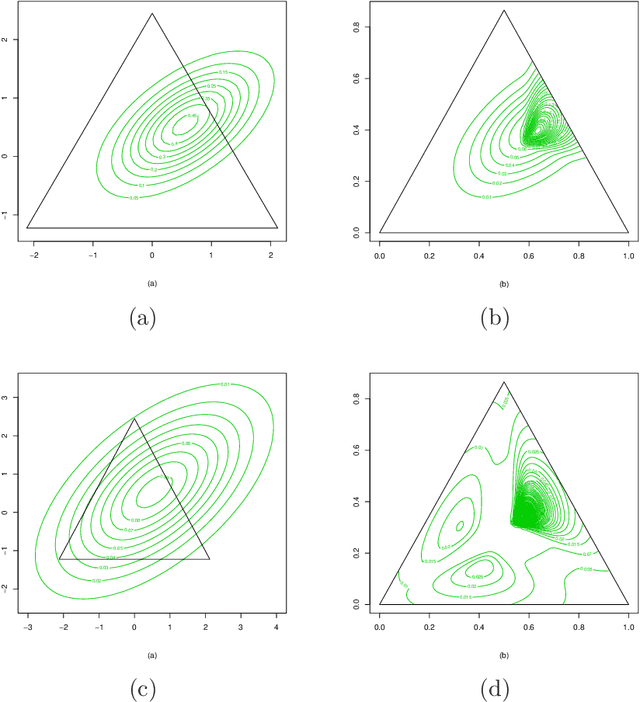
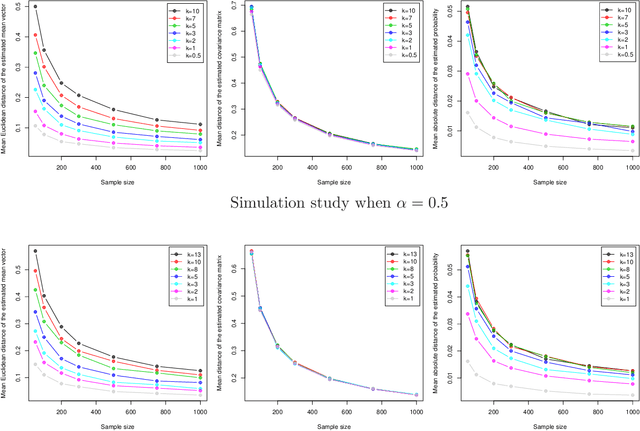
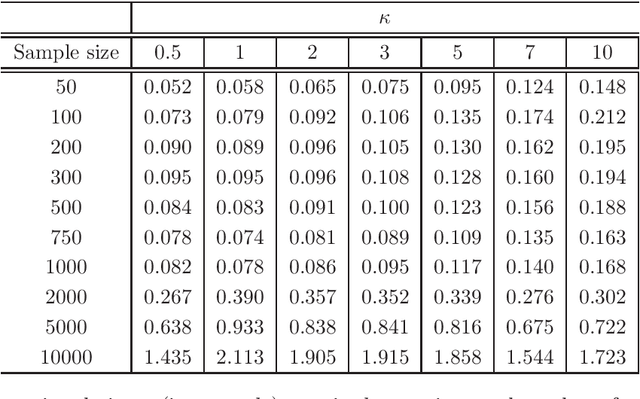
A folded type model is developed for analyzing compositional data. The proposed model, which is based upon the $\alpha$-transformation for compositional data, provides a new and flexible class of distributions for modeling data defined on the simplex sample space. Despite its rather seemingly complex structure, employment of the EM algorithm guarantees efficient parameter estimation. The model is validated through simulation studies and examples which illustrate that the proposed model performs better in terms of capturing the data structure, when compared to the popular logistic normal distribution.

Feature Selection with the R Package MXM: Discovering Statistically-Equivalent Feature Subsets

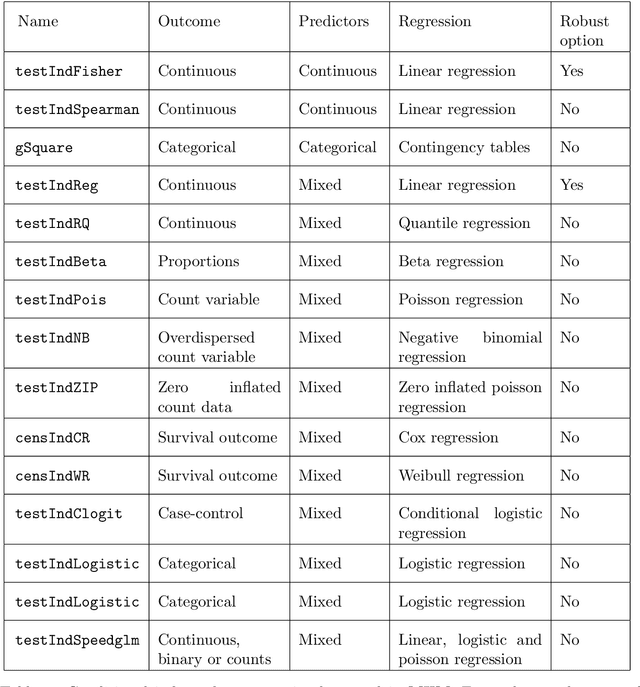
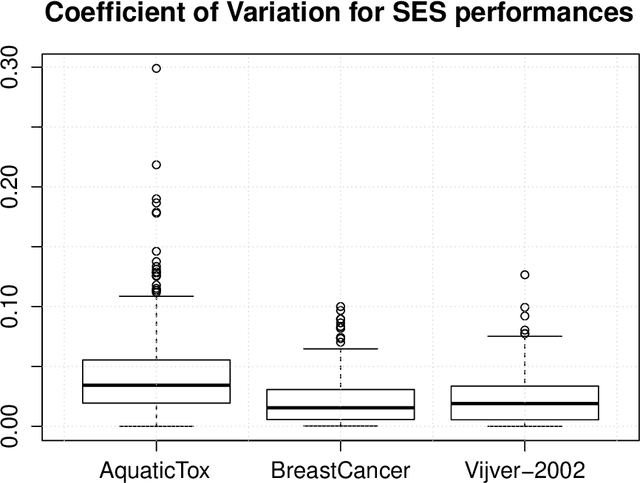
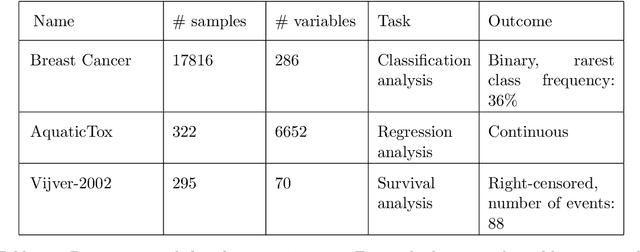
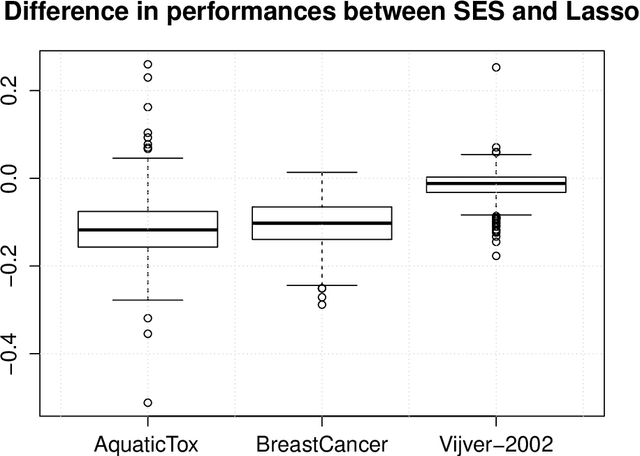
The statistically equivalent signature (SES) algorithm is a method for feature selection inspired by the principles of constrained-based learning of Bayesian Networks. Most of the currently available feature-selection methods return only a single subset of features, supposedly the one with the highest predictive power. We argue that in several domains multiple subsets can achieve close to maximal predictive accuracy, and that arbitrarily providing only one has several drawbacks. The SES method attempts to identify multiple, predictive feature subsets whose performances are statistically equivalent. Under that respect SES subsumes and extends previous feature selection algorithms, like the max-min parent children algorithm. SES is implemented in an homonym function included in the R package MXM, standing for mens ex machina, meaning 'mind from the machine' in Latin. The MXM implementation of SES handles several data-analysis tasks, namely classification, regression and survival analysis. In this paper we present the SES algorithm, its implementation, and provide examples of use of the SES function in R. Furthermore, we analyze three publicly available data sets to illustrate the equivalence of the signatures retrieved by SES and to contrast SES against the state-of-the-art feature selection method LASSO. Our results provide initial evidence that the two methods perform comparably well in terms of predictive accuracy and that multiple, equally predictive signatures are actually present in real world data.