To the Fairness Frontier and Beyond: Identifying, Quantifying, and Optimizing the Fairness-Accuracy Pareto Frontier

Algorithmic fairness has emerged as an important consideration when using machine learning to make high-stakes societal decisions. Yet, improved fairness often comes at the expense of model accuracy. While aspects of the fairness-accuracy tradeoff have been studied, most work reports the fairness and accuracy of various models separately; this makes model comparisons nearly impossible without a model-agnostic metric that reflects the balance of the two desiderata. We seek to identify, quantify, and optimize the empirical Pareto frontier of the fairness-accuracy tradeoff. Specifically, we identify and outline the empirical Pareto frontier through Tradeoff-between-Fairness-and-Accuracy (TAF) Curves; we then develop a metric to quantify this Pareto frontier through the weighted area under the TAF Curve which we term the Fairness-Area-Under-the-Curve (FAUC). TAF Curves provide the first empirical, model-agnostic characterization of the Pareto frontier, while FAUC provides the first metric to impartially compare model families on both fairness and accuracy. Both TAF Curves and FAUC can be employed with all group fairness definitions and accuracy measures. Next, we ask: Is it possible to expand the empirical Pareto frontier and thus improve the FAUC for a given collection of fitted models? We answer affirmately by developing a novel fair model stacking framework, FairStacks, that solves a convex program to maximize the accuracy of model ensemble subject to a score-bias constraint. We show that optimizing with FairStacks always expands the empirical Pareto frontier and improves the FAUC; we additionally study other theoretical properties of our proposed approach. Finally, we empirically validate TAF, FAUC, and FairStacks through studies on several real benchmark data sets, showing that FairStacks leads to major improvements in FAUC that outperform existing algorithmic fairness approaches.

A Coupled CP Decomposition for Principal Components Analysis of Symmetric Networks

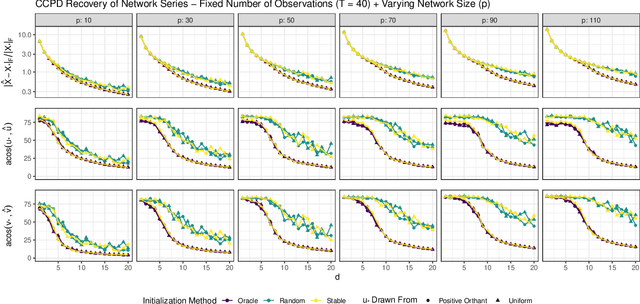
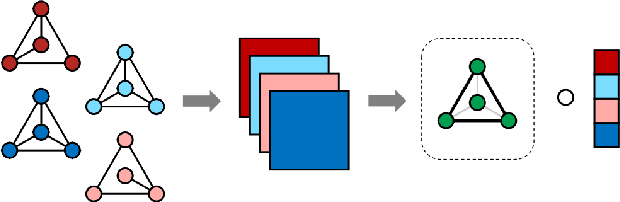
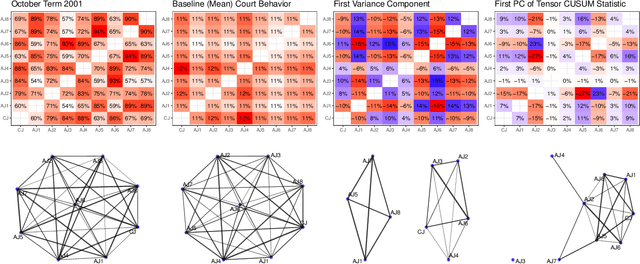
In a number of application domains, one observes a sequence of network data; for example, repeated measurements between users interactions in social media platforms, financial correlation networks over time, or across subjects, as in multi-subject studies of brain connectivity. One way to analyze such data is by stacking networks into a third-order array or tensor. We propose a principal components analysis (PCA) framework for sequence network data, based on a novel decomposition for semi-symmetric tensors. We derive efficient algorithms for computing our proposed "Coupled CP" decomposition and establish estimation consistency of our approach under an analogue of the spiked covariance model with rates the same as the matrix case up to a logarithmic term. Our framework inherits many of the strengths of classical PCA and is suitable for a wide range of unsupervised learning tasks, including identifying principal networks, isolating meaningful changepoints or outliers across observations, and for characterizing the "variability network" of the most varying edges. Finally, we demonstrate the effectiveness of our proposal on simulated data and on examples from political science and financial economics. The proof techniques used to establish our main consistency results are surprisingly straight-forward and may find use in a variety of other matrix and tensor decomposition problems.

Network Clustering for Latent State and Changepoint Detection

Network models provide a powerful and flexible framework for analyzing a wide range of structured data sources. In many situations of interest, however, multiple networks can be constructed to capture different aspects of an underlying phenomenon or to capture changing behavior over time. In such settings, it is often useful to cluster together related networks in attempt to identify patterns of common structure. In this paper, we propose a convex approach for the task of network clustering. Our approach uses a convex fusion penalty to induce a smoothly-varying tree-like cluster structure, eliminating the need to select the number of clusters a priori. We provide an efficient algorithm for convex network clustering and demonstrate its effectiveness on synthetic examples.

Sparse Partial Least Squares for Coarse Noisy Graph Alignment

Graph signal processing (GSP) provides a powerful framework for analyzing signals arising in a variety of domains. In many applications of GSP, multiple network structures are available, each of which captures different aspects of the same underlying phenomenon. To integrate these different data sources, graph alignment techniques attempt to find the best correspondence between vertices of two graphs. We consider a generalization of this problem, where there is no natural one-to-one mapping between vertices, but where there is correspondence between the community structures of each graph. Because we seek to learn structure at this higher community level, we refer to this problem as "coarse" graph alignment. To this end, we propose a novel regularized partial least squares method which both incorporates the observed graph structures and imposes sparsity in order to reflect the underlying block community structure. We provide efficient algorithms for our method and demonstrate its effectiveness in simulations.

Simultaneous Grouping and Denoising via Sparse Convex Wavelet Clustering

Clustering is a ubiquitous problem in data science and signal processing. In many applications where we observe noisy signals, it is common practice to first denoise the data, perhaps using wavelet denoising, and then to apply a clustering algorithm. In this paper, we develop a sparse convex wavelet clustering approach that simultaneously denoises and discovers groups. Our approach utilizes convex fusion penalties to achieve agglomeration and group-sparse penalties to denoise through sparsity in the wavelet domain. In contrast to common practice which denoises then clusters, our method is a unified, convex approach that performs both simultaneously. Our method yields denoised (wavelet-sparse) cluster centroids that both improve interpretability and data compression. We demonstrate our method on synthetic examples and in an application to NMR spectroscopy.

Automatic Registration and Convex Clustering of Time Series

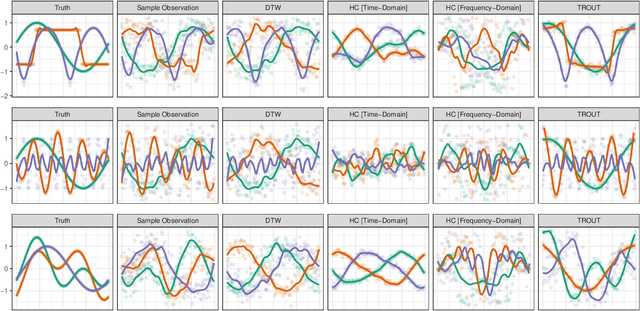
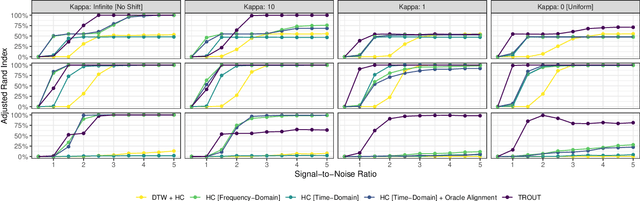
Clustering of time series data exhibits a number of challenges not present in other settings, notably the problem of registration (alignment) of observed signals. Typical approaches include pre-registration to a user-specified template or time warping approaches which attempt to optimally align series with a minimum of distortion. For many signals obtained from recording or sensing devices, these methods may be unsuitable as a template signal is not available for pre-registration, while the distortion of warping approaches may obscure meaningful temporal information. We propose a new method for automatic time series alignment within a convex clustering problem. Our approach, Temporal Registration using Optimal Unitary Transformations (TROUT), is based on a novel distance metric between time series that is easy to compute and automatically identifies optimal alignment between pairs of time series. By embedding our new metric in a convex formulation, we retain well-known advantages of computational and statistical performance. We provide an efficient algorithm for TROUT-based clustering and demonstrate its superior performance over a range of competitors.

Multi-Rank Sparse and Functional PCA: Manifold Optimization and Iterative Deflation Techniques

We consider the problem of estimating multiple principal components using the recently-proposed Sparse and Functional Principal Components Analysis (SFPCA) estimator. We first propose an extension of SFPCA which estimates several principal components simultaneously using manifold optimization techniques to enforce orthogonality constraints. While effective, this approach is computationally burdensome so we also consider iterative deflation approaches which take advantage of efficient algorithms for rank-one SFPCA. We show that alternative deflation schemes can more efficiently extract signal from the data, in turn improving estimation of subsequent components. Finally, we compare the performance of our manifold optimization and deflation techniques in a scenario where orthogonality does not hold and find that they still lead to significantly improved performance.

Splitting Methods for Convex Bi-Clustering and Co-Clustering

Co-Clustering, the problem of simultaneously identifying clusters across multiple aspects of a data set, is a natural generalization of clustering to higher-order structured data. Recent convex formulations of bi-clustering and tensor co-clustering, which shrink estimated centroids together using a convex fusion penalty, allow for global optimality guarantees and precise theoretical analysis, but their computational properties have been less well studied. In this note, we present three efficient operator-splitting methods for the convex co-clustering problem: a standard two-block ADMM, a Generalized ADMM which avoids an expensive tensor Sylvester equation in the primal update, and a three-block ADMM based on the operator splitting scheme of Davis and Yin. Theoretical complexity analysis suggests, and experimental evidence confirms, that the Generalized ADMM is far more efficient for large problems.

Dynamic Visualization and Fast Computation for Convex Clustering via Algorithmic Regularization

Convex clustering is a promising new approach to the classical problem of clustering, combining strong performance in empirical studies with rigorous theoretical foundations. Despite these advantages, convex clustering has not been widely adopted, due to its computationally intensive nature and its lack of compelling visualizations. To address these impediments, we introduce Algorithmic Regularization, an innovative technique for obtaining high-quality estimates of regularization paths using an iterative one-step approximation scheme. We justify our approach with a novel theoretical result, guaranteeing global convergence of the approximate path to the exact solution under easily-checked non-data-dependent assumptions. The application of algorithmic regularization to convex clustering yields the Convex Clustering via Algorithmic Regularization Paths (CARP) algorithm for computing the clustering solution path. On example data sets from genomics and text analysis, CARP delivers over a 100-fold speed-up over existing methods, while attaining a finer approximation grid than standard methods. Furthermore, CARP enables improved visualization of clustering solutions: the fine solution grid returned by CARP can be used to construct a convex clustering-based dendrogram, as well as forming the basis of a dynamic path-wise visualization based on modern web technologies. Our methods are implemented in the open-source R package clustRviz, available at https://github.com/DataSlingers/clustRviz.