A Transition-Aware Method for the Simulation of Compliant Contact with Regularized Friction

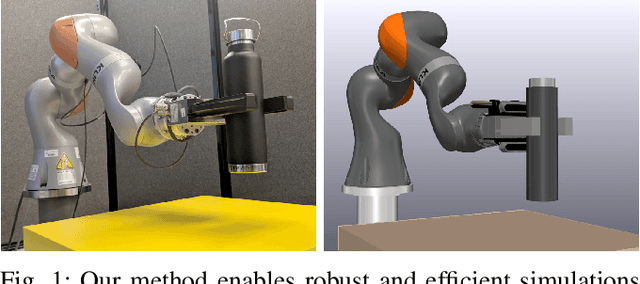
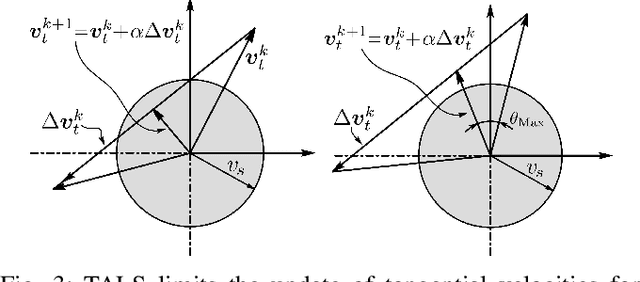
Multibody simulation with frictional contact has been a challenging subject of research for the past thirty years. Rigid-body assumptions are commonly used to approximate the physics of contact, and together with Coulomb friction, lead to challenging-to-solve nonlinear complementarity problems (NCP). On the other hand, robot grippers often introduce significant compliance. Compliant contact, combined with regularized friction, can be modeled entirely with ODEs, avoiding NCP solves. Unfortunately, regularized friction introduces high-frequency stiff dynamics and even implicit methods struggle with these systems, especially during slip-stick transitions. To improve the performance of implicit integration for these systems we introduce a Transition-Aware Line Search (TALS), which greatly improves the convergence of the Newton-Raphson iterations performed by implicit integrators. We find that TALS works best with semi-implicit integration, but that the explicit treatment of normal compliance can be problematic. To address this, we develop a Transition-Aware Modified Semi-Implicit (TAMSI) integrator that has similar computational cost to semi-implicit methods but implicitly couples compliant contact forces, leading to a more robust method. We evaluate the robustness, accuracy and performance of TAMSI and demonstrate our approach alongside a sim-to-real manipulation task.

A pressure field model for fast, robust approximation of net contact force and moment between nominally rigid objects

We introduce an approximate model for predicting the net contact wrench between nominally rigid objects for use in simulation, control, and state estimation. The model combines and generalizes two ideas: a bed of springs (an "elastic foundation") and hydrostatic pressure. In this model, continuous pressure fields are computed offline for the interior of each nominally rigid object. Unlike hydrostatics or elastic foundations, the pressure fields need not satisfy mechanical equilibrium conditions. When two objects nominally overlap, a contact surface is defined where the two pressure fields are equal. This static pressure is supplemented with a dissipative rate-dependent pressure and friction to determine tractions on the contact surface. The contact wrench between pairs of objects is an integral of traction contributions over this surface. The model evaluates much faster than elasticity-theory models, while showing the essential trends of force, moment, and stiffness increase with contact load. It yields continuous wrenches even for non-convex objects and coarse meshes. The method shows promise as sufficiently fast, accurate, and robust for design-in-simulation of robot controllers.