A pressure field model for fast, robust approximation of net contact force and moment between nominally rigid objects

We introduce an approximate model for predicting the net contact wrench between nominally rigid objects for use in simulation, control, and state estimation. The model combines and generalizes two ideas: a bed of springs (an "elastic foundation") and hydrostatic pressure. In this model, continuous pressure fields are computed offline for the interior of each nominally rigid object. Unlike hydrostatics or elastic foundations, the pressure fields need not satisfy mechanical equilibrium conditions. When two objects nominally overlap, a contact surface is defined where the two pressure fields are equal. This static pressure is supplemented with a dissipative rate-dependent pressure and friction to determine tractions on the contact surface. The contact wrench between pairs of objects is an integral of traction contributions over this surface. The model evaluates much faster than elasticity-theory models, while showing the essential trends of force, moment, and stiffness increase with contact load. It yields continuous wrenches even for non-convex objects and coarse meshes. The method shows promise as sufficiently fast, accurate, and robust for design-in-simulation of robot controllers.

Fundamental Limitations in Performance and Interpretability of Common Planar Rigid-Body Contact Models

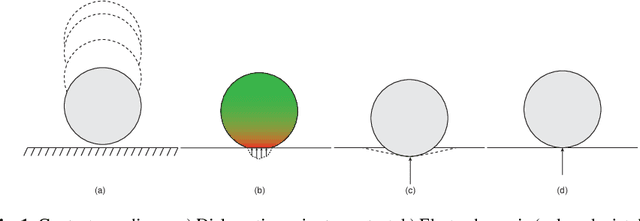
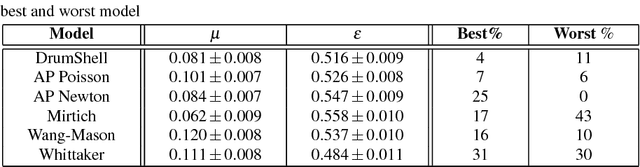
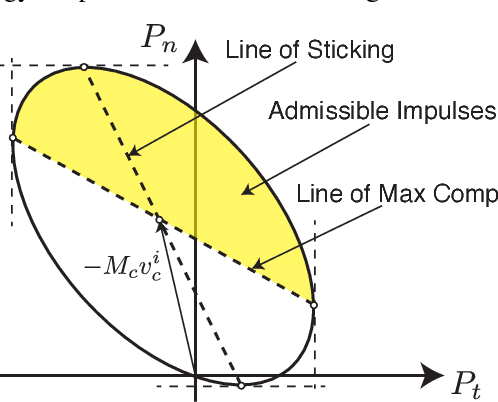
The ability to reason about and predict the outcome of contacts is paramount to the successful execution of many robot tasks. Analytical rigid-body contact models are used extensively in planning and control due to their computational efficiency and simplicity, yet despite their prevalence, little if any empirical comparison of these models has been made and it is unclear how well they approximate contact outcomes. In this paper, we first formulate a system identification approach for six commonly used contact models in the literature, and use the proposed method to find parameters for an experimental data-set of impacts. Next, we compare the models empirically, and establish a task specific upper bound on the performance of the models and the rigid-body contact model paradigm. We highlight the limitations of these models, salient failure modes, and the care that should be taken in parameter selection, which are ultimately difficult to give a physical interpretation.

Learning Data-Efficient Rigid-Body Contact Models: Case Study of Planar Impact

In this paper we demonstrate the limitations of common rigid-body contact models used in the robotics community by comparing them to a collection of data-driven and data-reinforced models that exploit underlying structure inspired by the rigid contact paradigm. We evaluate and compare the analytical and data-driven contact models on an empirical planar impact data-set, and show that the learned models are able to outperform their analytical counterparts with a small training set.

Particle Traces for Detecting Divergent Robot Behavior

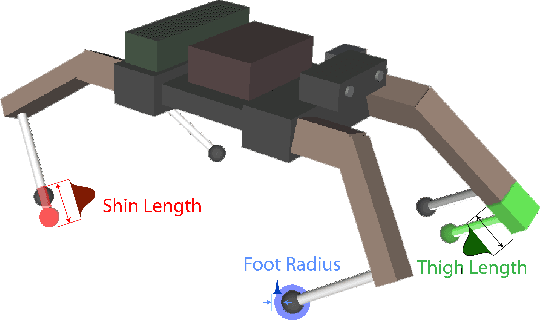
The motion of robots and objects in our world is often highly dependent upon contact. When contact is expected but does not occur or when contact is not expected but does occur, robot behavior diverges from plan, often disastrously. This paper describes an approach that uses simulation to detect possible such behavioral divergences on real robots. This approach, and others like it, could be applied to validation of robot behaviors, mechanism design, and even online planning. The particle trace approach samples robot modeling parameters, sensory readings, and state estimates to evaluate a robot's behavior statistically over a range of conditions. We demonstrate that combining even coarse estimates of state and modeling parameters with fast multibody simulation can be sufficient to detect divergent robot behavior and characterize robot performance in the real world. Correspondingly, this approach could be used to assess risk and find and analyze likely failures, given the extensive data that such simulations can generate. We assess this approach on actuated, high degree-of-freedom robot locomotion examples, a picking task with a fixed-base manipulator, and an unpowered passive dynamic walker. This research works toward understanding how multi-rigid body simulations can better characterize the behavior of robots without significantly compliant elements.

Inverse Dynamics with Rigid Contact and Friction

Inverse dynamics is used extensively in robotics and biomechanics applications. In manipulator and legged robots, it can form the basis of an effective nonlinear control strategy by providing a robot with both accurate positional tracking and active compliance. In biomechanics applications, inverse dynamics control can approximately determine the net torques applied at anatomical joints that correspond to an observed motion. In the context of robot control, using inverse dynamics requires knowledge of all contact forces acting on the robot; accurately perceiving external forces applied to the robot requires filtering and thus significant time delay. An alternative approach has been suggested in recent literature: predicting contact and actuator forces simultaneously under the assumptions of rigid body dynamics, rigid contact, and friction. Existing such inverse dynamics approaches have used approximations to the contact models, which permits use of fast numerical linear algebra algorithms. In contrast, we describe inverse dynamics algorithms that are derived only from first principles and use established phenomenological models like Coulomb friction. We assess these inverse dynamics algorithms in a control context using two virtual robots: a locomoting quadrupedal robot and a fixed-based manipulator gripping a box while using perfectly accurate sensor data from simulation. The data collected from these experiments gives an upper bound on the performance of such controllers in situ. For points of comparison, we assess performance on the same tasks with both error feedback control and inverse dynamics control with virtual contact force sensing.

Rapidly computable viscous friction and no-slip rigid contact models

This article presents computationally efficient algorithms for modeling two special cases of rigid contact---contact with only viscous friction and contact without slip---that have particularly useful applications in robotic locomotion and grasping. Modeling rigid contact with Coulomb friction generally exhibits $O(n^3)$ expected time complexity in the number of contact points and $2^{O(n)}$ worst-case complexity. The special cases we consider exhibit $O(m^3 + m^2n)$ time complexity ($m$ is the number of independent coordinates in the multi rigid body system) in the expected case and polynomial complexity in the worst case; thus, asymptotic complexity is no longer driven by number of contact points (which is conceivably limitless) but instead is more dependent on the number of bodies in the system (which is often fixed). These special cases also require considerably fewer constrained nonlinear optimization variables thus yielding substantial improvements in running time. Finally, these special cases also afford one other advantage: the nonlinear optimization problems are numerically easier to solve.