Graphcode: Learning from multiparameter persistent homology using graph neural networks

We introduce graphcodes, a novel multi-scale summary of the topological properties of a dataset that is based on the well-established theory of persistent homology. Graphcodes handle datasets that are filtered along two real-valued scale parameters. Such multi-parameter topological summaries are usually based on complicated theoretical foundations and difficult to compute; in contrast, graphcodes yield an informative and interpretable summary and can be computed as efficient as one-parameter summaries. Moreover, a graphcode is simply an embedded graph and can therefore be readily integrated in machine learning pipelines using graph neural networks. We describe such a pipeline and demonstrate that graphcodes achieve better classification accuracy than state-of-the-art approaches on various datasets.

Topological Data Analysis in smart manufacturing processes -- A survey on the state of the art

Topological Data Analysis (TDA) is a mathematical method using techniques from topology for the analysis of complex, multi-dimensional data that has been widely and successfully applied in several fields such as medicine, material science, biology, and others. This survey summarizes the state of the art of TDA in yet another application area: industrial manufacturing and production in the context of Industry 4.0. We perform a rigorous and reproducible literature search of applications of TDA on the setting of industrial production and manufacturing. The resulting works are clustered and analyzed based on their application area within the manufacturing process and their input data type. We highlight the key benefits of TDA and their tools in this area and describe its challenges, as well as future potential. Finally, we discuss which TDA methods are underutilized in (the specific area of) industry and the identified types of application, with the goal of prompting more research in this profitable area of application.

A Kernel for Multi-Parameter Persistent Homology

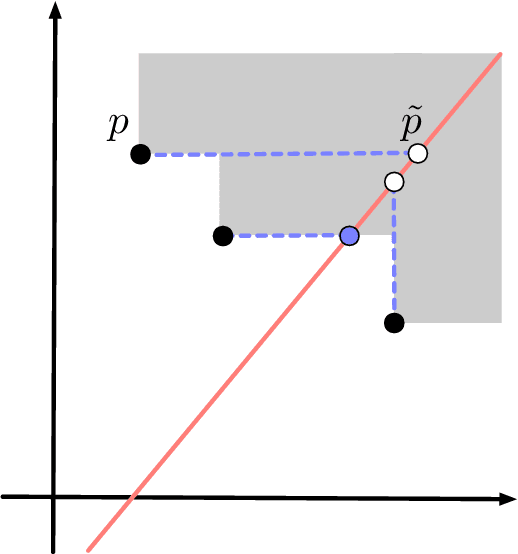
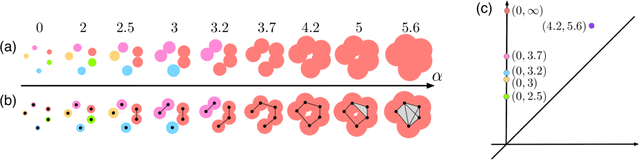
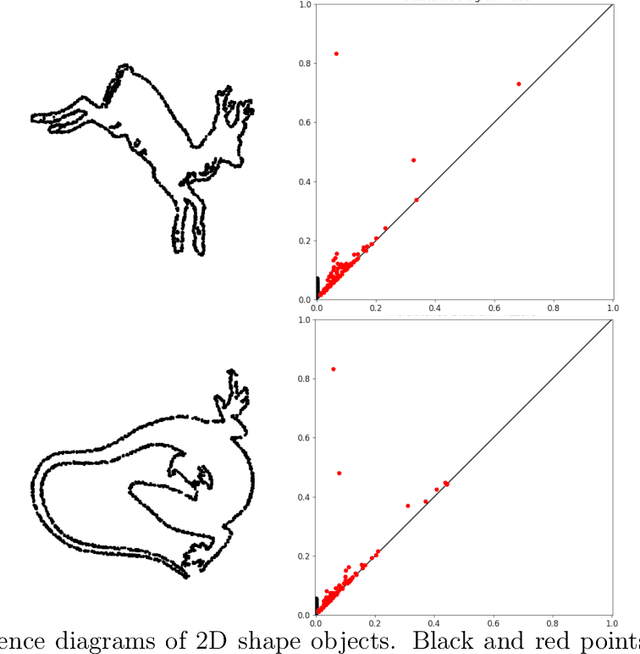
Topological data analysis and its main method, persistent homology, provide a toolkit for computing topological information of high-dimensional and noisy data sets. Kernels for one-parameter persistent homology have been established to connect persistent homology with machine learning techniques. We contribute a kernel construction for multi-parameter persistence by integrating a one-parameter kernel weighted along straight lines. We prove that our kernel is stable and efficiently computable, which establishes a theoretical connection between topological data analysis and machine learning for multivariate data analysis.