Approximating Defeasible Logics to Improve Scalability

Defeasible rules are used in providing computable representations of legal documents and, more recently, have been suggested as a basis for explainable AI. Such applications draw attention to the scalability of implementations. The defeasible logic $DL(\partial_{||})$ was introduced as a more scalable alternative to $DL(\partial)$, which is better known. In this paper we consider the use of (implementations of) $DL(\partial_{||})$ as a computational aid to computing conclusions in $DL(\partial)$ and other defeasible logics, rather than as an alternative to $DL(\partial)$. We identify conditions under which $DL(\partial_{||})$ can be substituted for $DL(\partial)$ with no change to the conclusions drawn, and conditions under which $DL(\partial_{||})$ can be used to draw some valid conclusions, leaving the remainder to be drawn by $DL(\partial)$.

Defeasible Reasoning via Datalog$^ eg$

We address the problem of compiling defeasible theories to Datalog$^\neg$ programs. We prove the correctness of this compilation, for the defeasible logic $DL(\partial_{||})$, but the techniques we use apply to many other defeasible logics. Structural properties of $DL(\partial_{||})$ are identified that support efficient implementation and/or approximation of the conclusions of defeasible theories in the logic, compared with other defeasible logics. We also use previously well-studied structural properties of logic programs to adapt to incomplete Datalog$^\neg$ implementations.

Relative Expressiveness of Defeasible Logics II

(Maher 2012) introduced an approach for relative expressiveness of defeasible logics, and two notions of relative expressiveness were investigated. Using the first of these definitions of relative expressiveness, we show that all the defeasible logics in the DL framework are equally expressive under this formulation of relative expressiveness. The second formulation of relative expressiveness is stronger than the first. However, we show that logics incorporating individual defeat are equally expressive as the corresponding logics with team defeat. Thus the only differences in expressiveness of logics in DL arise from differences in how ambiguity is handled. This completes the study of relative expressiveness in DL begun in \cite{Maher12}.

Corruption and Audit in Strategic Argumentation

Strategic argumentation provides a simple model of disputation and negotiation among agents. Although agents might be expected to act in our best interests, there is little that enforces such behaviour. (Maher, 2016) introduced a model of corruption and resistance to corruption within strategic argumentation. In this paper we identify corrupt behaviours that are not detected in that formulation. We strengthen the model to detect such behaviours, and show that, under the strengthened model, all the strategic aims in (Maher, 2016) are resistant to corruption.

Contractibility for Open Global Constraints

Open forms of global constraints allow the addition of new variables to an argument during the execution of a constraint program. Such forms are needed for difficult constraint programming problems where problem construction and problem solving are interleaved, and fit naturally within constraint logic programming. However, in general, filtering that is sound for a global constraint can be unsound when the constraint is open. This paper provides a simple characterization, called contractibility, of the constraints where filtering remains sound when the constraint is open. With this characterization we can easily determine whether a constraint has this property or not. In the latter case, we can use it to derive a contractible approximation to the constraint. We demonstrate this work on both hard and soft constraints. In the process, we formulate two general classes of soft constraints.

Flow-Based Propagators for the SEQUENCE and Related Global Constraints

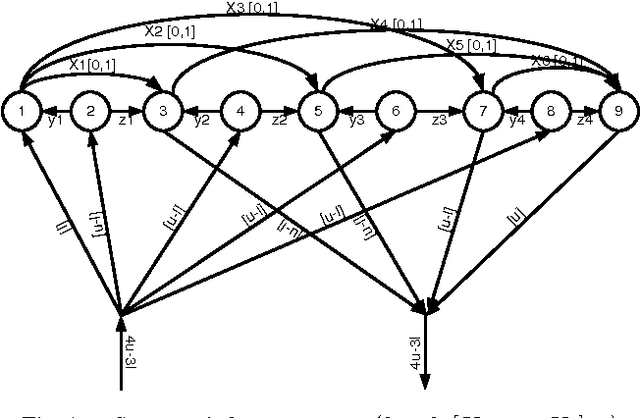
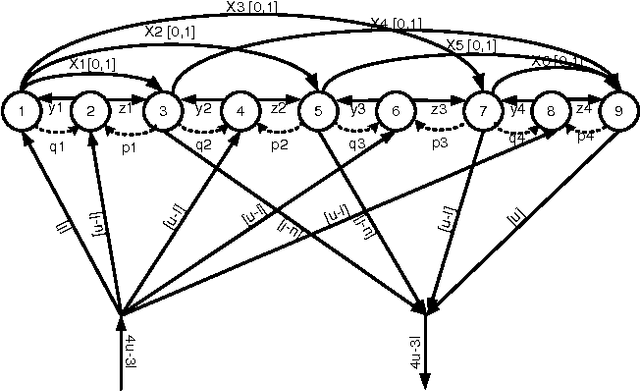
We propose new filtering algorithms for the SEQUENCE constraint and some extensions of the SEQUENCE constraint based on network flows. We enforce domain consistency on the SEQUENCE constraint in $O(n^2)$ time down a branch of the search tree. This improves upon the best existing domain consistency algorithm by a factor of $O(\log n)$. The flows used in these algorithms are derived from a linear program. Some of them differ from the flows used to propagate global constraints like GCC since the domains of the variables are encoded as costs on the edges rather than capacities. Such flows are efficient for maintaining bounds consistency over large domains and may be useful for other global constraints.

Propositional Defeasible Logic has Linear Complexity

Defeasible logic is a rule-based nonmonotonic logic, with both strict and defeasible rules, and a priority relation on rules. We show that inference in the propositional form of the logic can be performed in linear time. This contrasts markedly with most other propositional nonmonotonic logics, in which inference is intractable.