Flow-Based Propagators for the SEQUENCE and Related Global Constraints

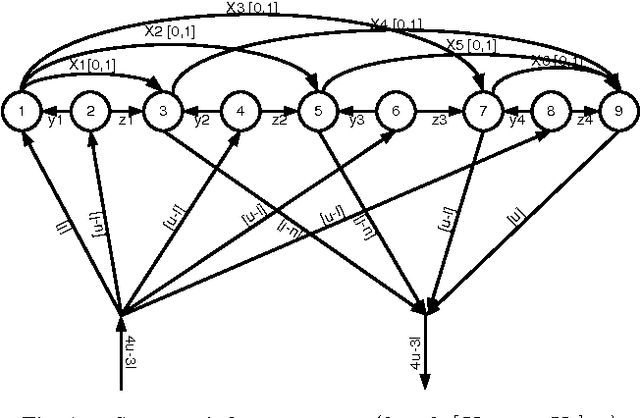
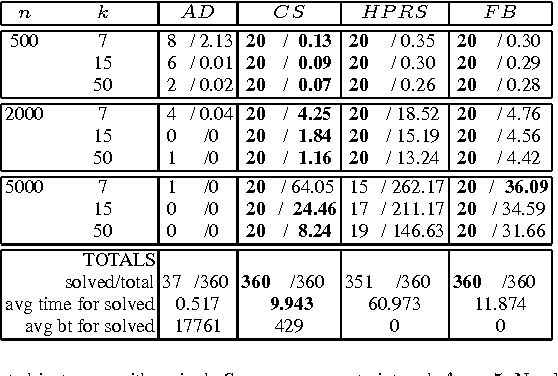
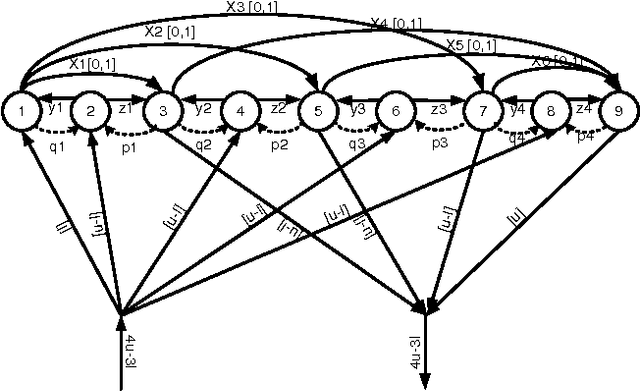
We propose new filtering algorithms for the SEQUENCE constraint and some extensions of the SEQUENCE constraint based on network flows. We enforce domain consistency on the SEQUENCE constraint in $O(n^2)$ time down a branch of the search tree. This improves upon the best existing domain consistency algorithm by a factor of $O(\log n)$. The flows used in these algorithms are derived from a linear program. Some of them differ from the flows used to propagate global constraints like GCC since the domains of the variables are encoded as costs on the edges rather than capacities. Such flows are efficient for maintaining bounds consistency over large domains and may be useful for other global constraints.