Multitask methods for predicting molecular properties from heterogeneous data

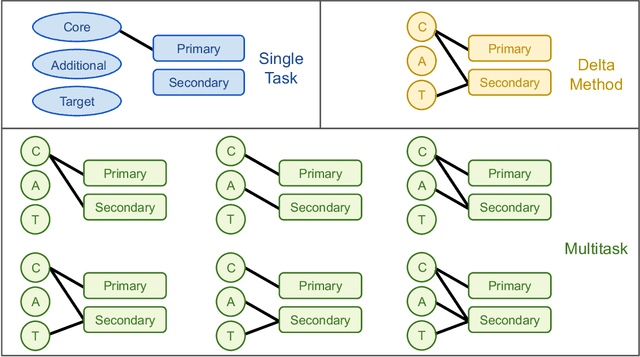
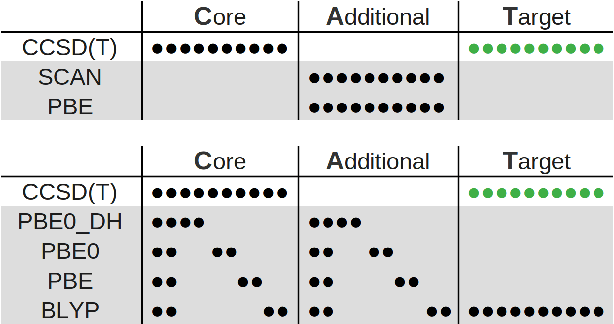
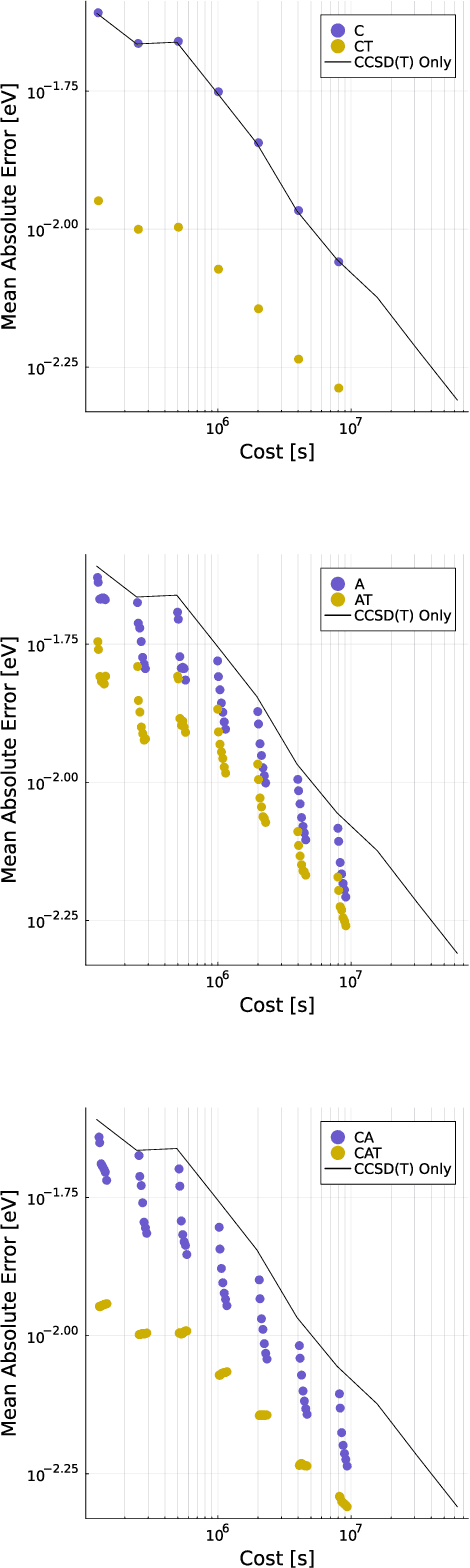
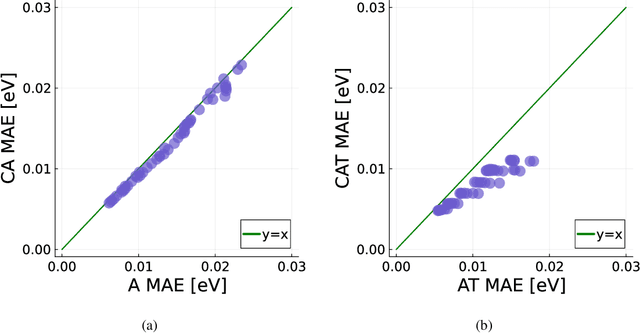
Data generation remains a bottleneck in training surrogate models to predict molecular properties. We demonstrate that multitask Gaussian process regression overcomes this limitation by leveraging both expensive and cheap data sources. In particular, we consider training sets constructed from coupled-cluster (CC) and density function theory (DFT) data. We report that multitask surrogates can predict at CC level accuracy with a reduction to data generation cost by over an order of magnitude. Of note, our approach allows the training set to include DFT data generated by a heterogeneous mix of exchange-correlation functionals without imposing any artificial hierarchy on functional accuracy. More generally, the multitask framework can accommodate a wider range of training set structures -- including full disparity between the different levels of fidelity -- than existing kernel approaches based on $\Delta$-learning, though we show that the accuracy of the two approaches can be similar. Consequently, multitask regression can be a tool for reducing data generation costs even further by opportunistically exploiting existing data sources.

Rotationally Equivariant Neural Operators for Learning Transformations on Tensor Fields (eg 3D Images and Vector Fields)

We introduce equivariant neural operators for learning resolution invariant as well as translation and rotation equivariant transformations between sets of tensor fields. Input and output may contain arbitrary mixes of scalar fields, vector fields, second order tensor fields and higher order fields. Our tensor field convolution layers emulate any linear operator by learning its impulse response or Green's function as the convolution kernel. Our tensor field attention layers emulate pairwise field coupling via local tensor products. Convolutions and associated adjoints can be in real or Fourier space allowing for linear scaling. By unifying concepts from E3NN, TBNN and FNO, we achieve good predictive performance on a wide range of PDEs and dynamical systems in engineering and quantum chemistry. Code is in Julia and available upon request from authors.