Deep Q-learning of global optimizer of multiply model parameters for viscoelastic imaging

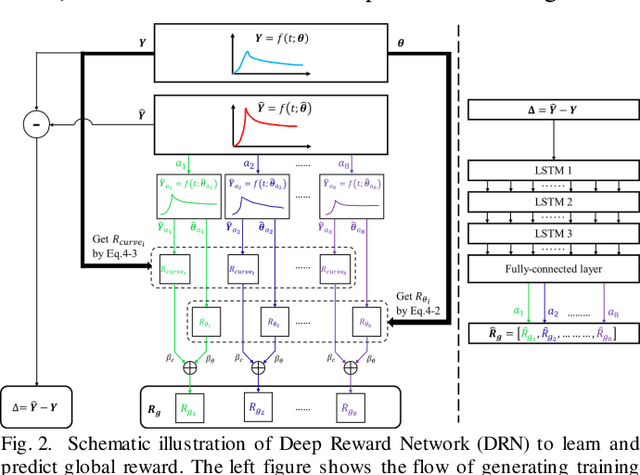
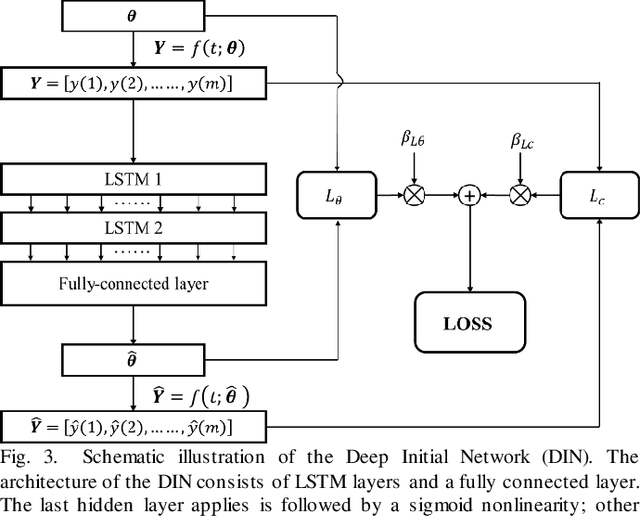
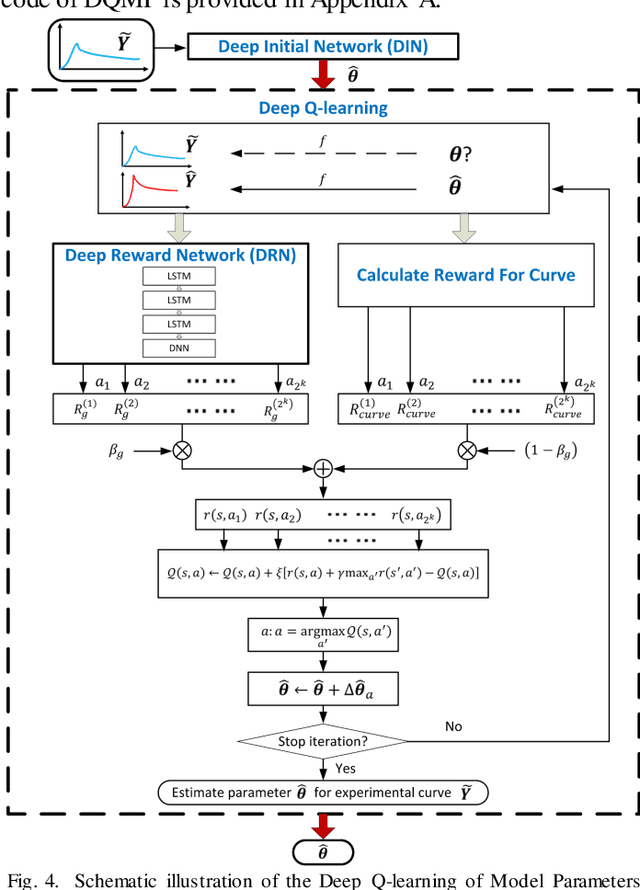
Objective: Estimation of the global optima of multiple model parameters is valuable in imaging to form a reliable diagnostic image. Given non convexity of the objective function, it is challenging to avoid from different local minima. Methods: We first formulate the global searching of multiply parameters to be a k-D move in the parametric space, and convert parameters updating to be state-action decision-making problem. We proposed a novel Deep Q-learning of Model Parameters (DQMP) method for global optimization of model parameters by updating the parameter configurations through actions that maximize a Q-value, which employs a Deep Reward Network designed to learn global reward values from both visible curve fitting errors and hidden parameter errors. Results: The DQMP method was evaluated by viscoelastic imaging on soft matter by Kelvin-Voigt fractional derivative (KVFD) modeling. In comparison to other methods, imaging of parameters by DQMP yielded the smallest errors (< 2%) to the ground truth images. DQMP was applied to viscoelastic imaging on biological tissues, which indicated a great potential of imaging on physical parameters in diagnostic applications. Conclusions: DQMP method is able to achieve global optima, yielding accurate model parameter estimates in viscoelastic imaging. Assessment of DQMP by simulation imaging and ultrasound breast imaging demonstrated the consistency, reliability of the imaged parameters, and powerful global searching ability of DQMP. Significance: DQMP method is promising for imaging of multiple parameters, and can be generalized to global optimization for many other complex nonconvex functions and imaging of physical parameters.

Cartesian Neural Network Constitutive Models for Data-driven Elasticity Imaging

Elasticity images map biomechanical properties of soft tissues to aid in the detection and diagnosis of pathological states. In particular, quasi-static ultrasonic (US) elastography techniques use force-displacement measurements acquired during an US scan to parameterize the spatio-temporal stress-strain behavior. Current methods use a model-based inverse approach to estimate the parameters associated with a chosen constitutive model. However, model-based methods rely on simplifying assumptions of tissue biomechanical properties, often limiting elastography to imaging one or two linear-elastic parameters. We previously described a data-driven method for building neural network constitutive models (NNCMs) that learn stress-strain relationships from force-displacement data. Using measurements acquired on gelatin phantoms, we demonstrated the ability of NNCMs to characterize linear-elastic mechanical properties without an initial model assumption and thus circumvent the mathematical constraints typically encountered in classic model-based approaches to the inverse problem. While successful, we were required to use a priori knowledge of the internal object shape to define the spatial distribution of regions exhibiting different material properties. Here, we introduce Cartesian neural network constitutive models (CaNNCMs) that are capable of using data to model both linear-elastic mechanical properties and their distribution in space. We demonstrate the ability of CaNNCMs to capture arbitrary material property distributions using stress-strain data from simulated phantoms. Furthermore, we show that a trained CaNNCM can be used to reconstruct a Young's modulus image. CaNNCMs are an important step toward data-driven modeling and imaging the complex mechanical properties of soft tissues.