Learning Rate Matters: Vanilla LoRA May Suffice for LLM Fine-tuning

Low-Rank Adaptation (LoRA) is the prevailing approach for efficient large language model (LLM) fine-tuning. Building on this paradigm, recent studies have proposed alternative initialization strategies and architectural modifications, reporting substantial improvements over vanilla LoRA. However, these gains are often demonstrated under fixed or narrowly tuned hyperparameter settings, despite the known sensitivity of neural networks to training configurations. In this work, we systematically re-evaluate four representative LoRA variants alongside vanilla LoRA through extensive hyperparameter searches. Across mathematical and code generation tasks on diverse model scales, we find that different LoRA methods favor distinct learning rate ranges. Crucially, once learning rates are properly tuned, all methods achieve similar peak performance (within 1-2%), with only subtle rank-dependent behaviors. These results suggest that vanilla LoRA remains a competitive baseline and that improvements reported under single training configuration may not reflect consistent methodological advantages. Finally, a second-order analysis attributes the differing optimal learning rate ranges to variations in the largest Hessian eigenvalue, aligning with classical learning theories.

Accelerating Continuous Normalizing Flow with Trajectory Polynomial Regularization

In this paper, we propose an approach to effectively accelerating the computation of continuous normalizing flow (CNF), which has been proven to be a powerful tool for the tasks such as variational inference and density estimation. The training time cost of CNF can be extremely high because the required number of function evaluations (NFE) for solving corresponding ordinary differential equations (ODE) is very large. We think that the high NFE results from large truncation errors of solving ODEs. To address the problem, we propose to add a regularization. The regularization penalizes the difference between the trajectory of the ODE and its fitted polynomial regression. The trajectory of ODE will approximate a polynomial function, and thus the truncation error will be smaller. Furthermore, we provide two proofs and claim that the additional regularization does not harm training quality. Experimental results show that our proposed method can result in 42.3% to 71.3% reduction of NFE on the task of density estimation, and 19.3% to 32.1% reduction of NFE on variational auto-encoder, while the testing losses are not affected at all.

Attribute-aware Collaborative Filtering: Survey and Classification

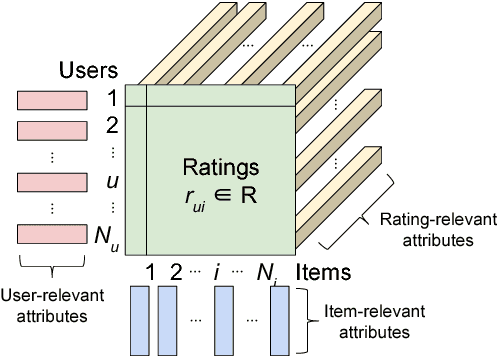
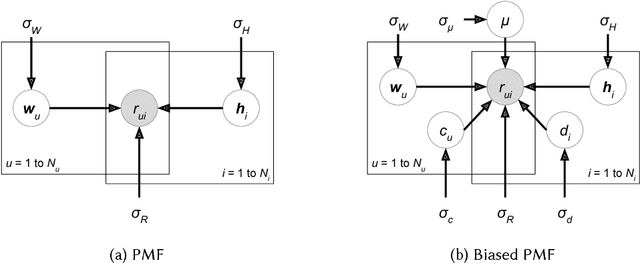
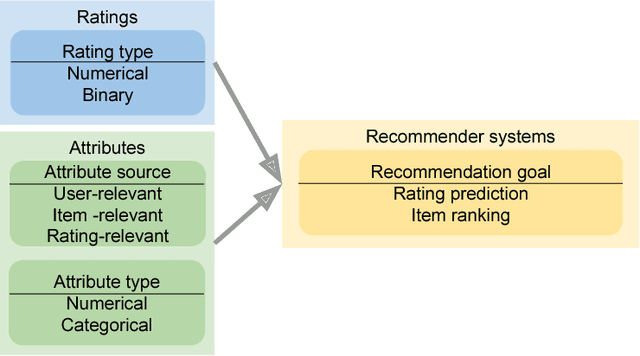
Attribute-aware CF models aims at rating prediction given not only the historical rating from users to items, but also the information associated with users (e.g. age), items (e.g. price), or even ratings (e.g. rating time). This paper surveys works in the past decade developing attribute-aware CF systems, and discovered that mathematically they can be classified into four different categories. We provide the readers not only the high level mathematical interpretation of the existing works in this area but also the mathematical insight for each category of models. Finally we provide in-depth experiment results comparing the effectiveness of the major works in each category.