Winner-Take-All Computation in Spiking Neural Networks

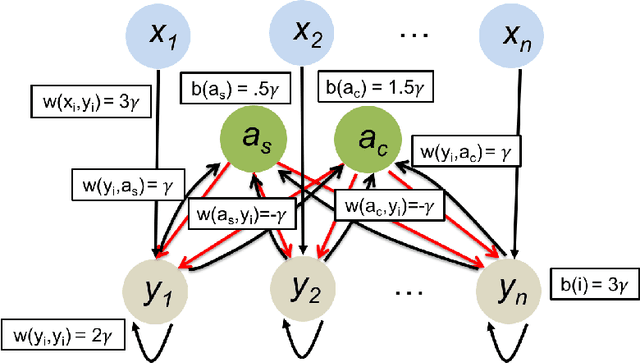
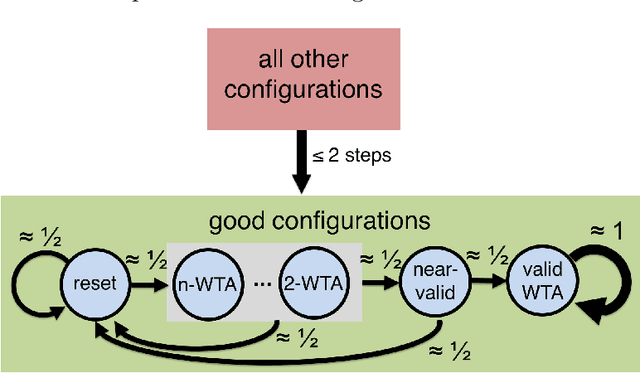
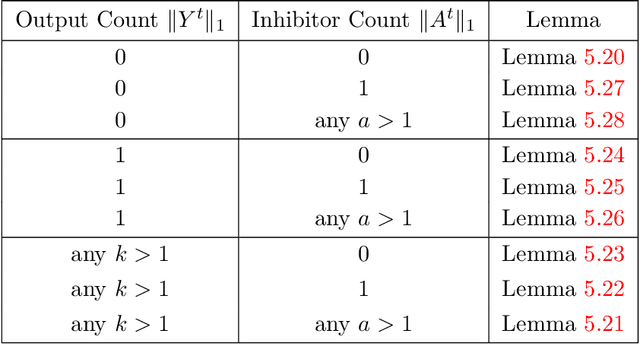
In this work we study biological neural networks from an algorithmic perspective, focusing on understanding tradeoffs between computation time and network complexity. Our goal is to abstract real neural networks in a way that, while not capturing all interesting features, preserves high-level behavior and allows us to make biologically relevant conclusions. Towards this goal, we consider the implementation of algorithmic primitives in a simple yet biologically plausible model of $stochastic\ spiking\ neural\ networks$. In particular, we show how the stochastic behavior of neurons in this model can be leveraged to solve a basic $symmetry-breaking\ task$ in which we are given neurons with identical firing rates and want to select a distinguished one. In computational neuroscience, this is known as the winner-take-all (WTA) problem, and it is believed to serve as a basic building block in many tasks, e.g., learning, pattern recognition, and clustering. We provide efficient constructions of WTA circuits in our stochastic spiking neural network model, as well as lower bounds in terms of the number of auxiliary neurons required to drive convergence to WTA in a given number of steps. These lower bounds demonstrate that our constructions are near-optimal in some cases. This work covers and gives more in-depth proofs of a subset of results originally published in [LMP17a]. It is adapted from the last chapter of C. Musco's Ph.D. thesis [Mus18].

Counting to Ten with Two Fingers: Compressed Counting with Spiking Neurons

We consider the task of measuring time with probabilistic threshold gates implemented by bio-inspired spiking neurons. In the model of spiking neural networks, network evolves in discrete rounds, where in each round, neurons fire in pulses in response to a sufficiently high membrane potential. This potential is induced by spikes from neighboring neurons that fired in the previous round, which can have either an excitatory or inhibitory effect. We first consider a deterministic implementation of a neural timer and show that $\Theta(\log t)$ (deterministic) threshold gates are both sufficient and necessary. This raised the question of whether randomness can be leveraged to reduce the number of neurons. We answer this question in the affirmative by considering neural timers with spiking neurons where the neuron $y$ is required to fire for $t$ consecutive rounds with probability at least $1-\delta$, and should stop firing after at most $2t$ rounds with probability $1-\delta$ for some input parameter $\delta \in (0,1)$. Our key result is a construction of a neural timer with $O(\log\log 1/\delta)$ spiking neurons. Interestingly, this construction uses only one spiking neuron, while the remaining neurons can be deterministic threshold gates. We complement this construction with a matching lower bound of $\Omega(\min\{\log\log 1/\delta, \log t\})$ neurons. This provides the first separation between deterministic and randomized constructions in the setting of spiking neural networks. Finally, we demonstrate the usefulness of compressed counting networks for synchronizing neural networks.

Neuro-RAM Unit with Applications to Similarity Testing and Compression in Spiking Neural Networks

We study distributed algorithms implemented in a simplified biologically inspired model for stochastic spiking neural networks. We focus on tradeoffs between computation time and network complexity, along with the role of randomness in efficient neural computation. It is widely accepted that neural computation is inherently stochastic. In recent work, we explored how this stochasticity could be leveraged to solve the `winner-take-all' leader election task. Here, we focus on using randomness in neural algorithms for similarity testing and compression. In the most basic setting, given two $n$-length patterns of firing neurons, we wish to distinguish if the patterns are equal or $\epsilon$-far from equal. Randomization allows us to solve this task with a very compact network, using $O \left (\frac{\sqrt{n}\log n}{\epsilon}\right)$ auxiliary neurons, which is sublinear in the input size. At the heart of our solution is the design of a $t$-round neural random access memory, or indexing network, which we call a neuro-RAM. This module can be implemented with $O(n/t)$ auxiliary neurons and is useful in many applications beyond similarity testing. Using a VC dimension-based argument, we show that the tradeoff between runtime and network size in our neuro-RAM is nearly optimal. Our result has several implications -- since our neuro-RAM can be implemented with deterministic threshold gates, it shows that, in contrast to similarity testing, randomness does not provide significant computational advantages for this problem. It also establishes a separation between feedforward networks whose gates spike with sigmoidal probability functions, and well-studied deterministic sigmoidal networks, whose gates output real number sigmoidal values, and which can implement a neuro-RAM much more efficiently.

Computational Tradeoffs in Biological Neural Networks: Self-Stabilizing Winner-Take-All Networks

We initiate a line of investigation into biological neural networks from an algorithmic perspective. We develop a simplified but biologically plausible model for distributed computation in stochastic spiking neural networks and study tradeoffs between computation time and network complexity in this model. Our aim is to abstract real neural networks in a way that, while not capturing all interesting features, preserves high-level behavior and allows us to make biologically relevant conclusions. In this paper, we focus on the important `winner-take-all' (WTA) problem, which is analogous to a neural leader election unit: a network consisting of $n$ input neurons and $n$ corresponding output neurons must converge to a state in which a single output corresponding to a firing input (the `winner') fires, while all other outputs remain silent. Neural circuits for WTA rely on inhibitory neurons, which suppress the activity of competing outputs and drive the network towards a converged state with a single firing winner. We attempt to understand how the number of inhibitors used affects network convergence time. We show that it is possible to significantly outperform naive WTA constructions through a more refined use of inhibition, solving the problem in $O(\theta)$ rounds in expectation with just $O(\log^{1/\theta} n)$ inhibitors for any $\theta$. An alternative construction gives convergence in $O(\log^{1/\theta} n)$ rounds with $O(\theta)$ inhibitors. We compliment these upper bounds with our main technical contribution, a nearly matching lower bound for networks using $\ge \log\log n$ inhibitors. Our lower bound uses familiar indistinguishability and locality arguments from distributed computing theory. It lets us derive a number of interesting conclusions about the structure of any network solving WTA with good probability, and the use of randomness and inhibition within such a network.