Mengyi Yan
Stacked Kernel Network
Nov 25, 2017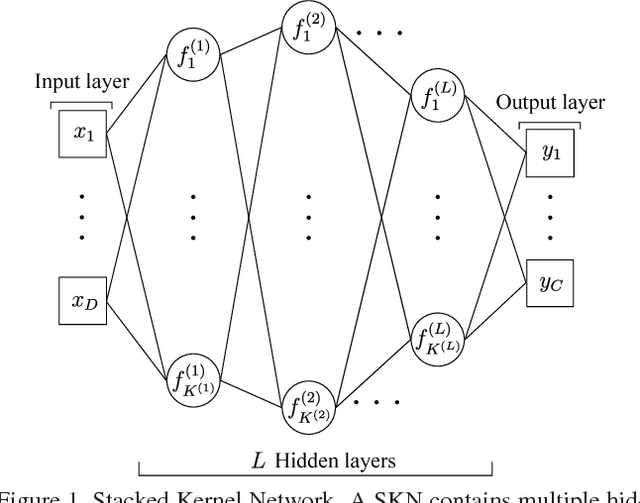
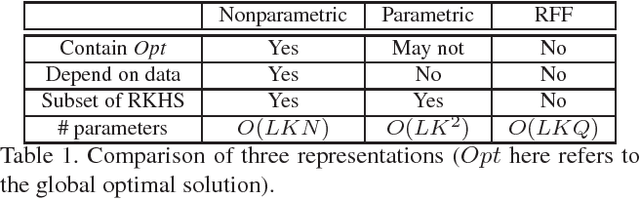
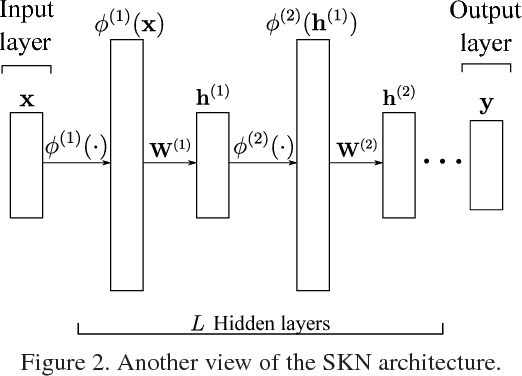
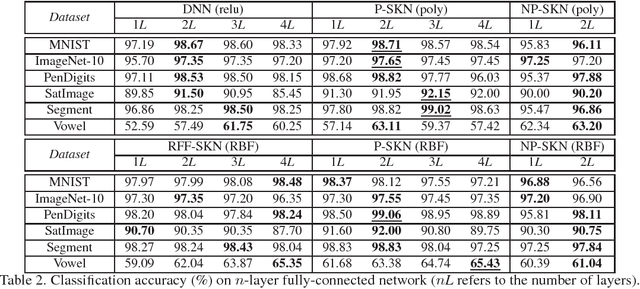
Abstract:Kernel methods are powerful tools to capture nonlinear patterns behind data. They implicitly learn high (even infinite) dimensional nonlinear features in the Reproducing Kernel Hilbert Space (RKHS) while making the computation tractable by leveraging the kernel trick. Classic kernel methods learn a single layer of nonlinear features, whose representational power may be limited. Motivated by recent success of deep neural networks (DNNs) that learn multi-layer hierarchical representations, we propose a Stacked Kernel Network (SKN) that learns a hierarchy of RKHS-based nonlinear features. SKN interleaves several layers of nonlinear transformations (from a linear space to a RKHS) and linear transformations (from a RKHS to a linear space). Similar to DNNs, a SKN is composed of multiple layers of hidden units, but each parameterized by a RKHS function rather than a finite-dimensional vector. We propose three ways to represent the RKHS functions in SKN: (1)nonparametric representation, (2)parametric representation and (3)random Fourier feature representation. Furthermore, we expand SKN into CNN architecture called Stacked Kernel Convolutional Network (SKCN). SKCN learning a hierarchy of RKHS-based nonlinear features by convolutional operation with each filter also parameterized by a RKHS function rather than a finite-dimensional matrix in CNN, which is suitable for image inputs. Experiments on various datasets demonstrate the effectiveness of SKN and SKCN, which outperform the competitive methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge