Learning Graph Filters for Structure-Function Coupling based Hub Node Identification

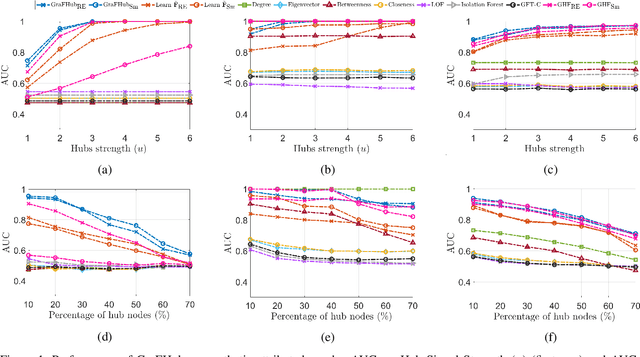
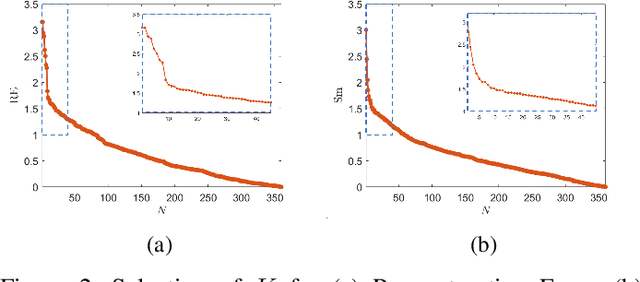
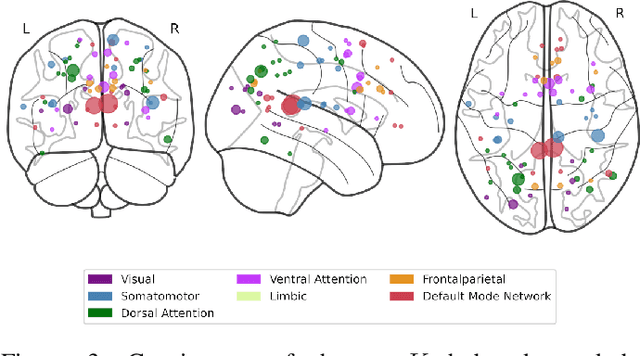
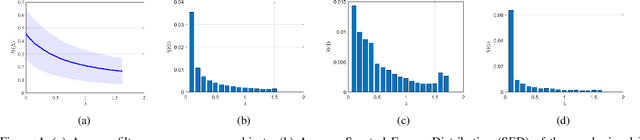
Over the past two decades, tools from network science have been leveraged to characterize the organization of both structural and functional networks of the brain. One such measure of network organization is hub node identification. Hubs are specialized nodes within a network that link distinct brain units corresponding to specialized functional processes. Conventional methods for identifying hub nodes utilize different types of centrality measures and participation coefficient to profile various aspects of nodal importance. These methods solely rely on the functional connectivity networks constructed from functional magnetic resonance imaging (fMRI), ignoring the structure-function coupling in the brain. In this paper, we introduce a graph signal processing (GSP) based hub detection framework that utilizes both the structural connectivity and the functional activation to identify hub nodes. The proposed framework models functional activity as graph signals on the structural connectivity. Hub nodes are then detected based on the premise that hub nodes are sparse, have higher level of activity compared to their neighbors, and the non-hub nodes' activity can be modeled as the output of a graph-based filter. Based on these assumptions, an optimization framework, GraFHub, is formulated to learn the coefficients of the optimal polynomial graph filter and detect the hub nodes. The proposed framework is evaluated on both simulated data and resting state fMRI (rs-fMRI) data from Human Connectome Project (HCP).

Optimal Graph Filters for Clustering Attributed Graphs

Many real-world systems can be represented as graphs where the different entities are presented by nodes and their interactions by edges. An important task in studying large datasets is graph clustering. While there has been a lot of work on graph clustering using the connectivity between the nodes, many real-world networks also have node attributes. Clustering attributed graphs requires joint modeling of graph structure and node attributes. Recent work has focused on graph convolutional networks and graph convolutional filters to combine structural and content information. However, these methods are mostly limited to lowpass filtering and do not explicitly optimize the filters for the clustering task. In this paper, we introduce a graph signal processing based approach, where we design polynomial graph filters optimized for clustering. The proposed approach is formulated as a two-step iterative optimization problem where graph filters that are interpretable and optimal for the given data are learned while maximizing the separation between different clusters. The proposed approach is evaluated on attributed networks and compared to the state-of-the-art graph convolutional network approaches.

Community Detection in Multi-frequency EEG Networks

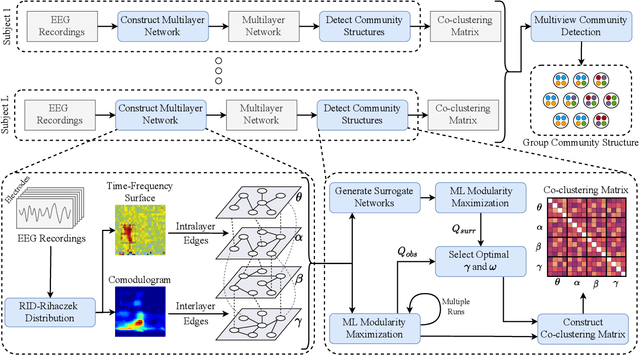
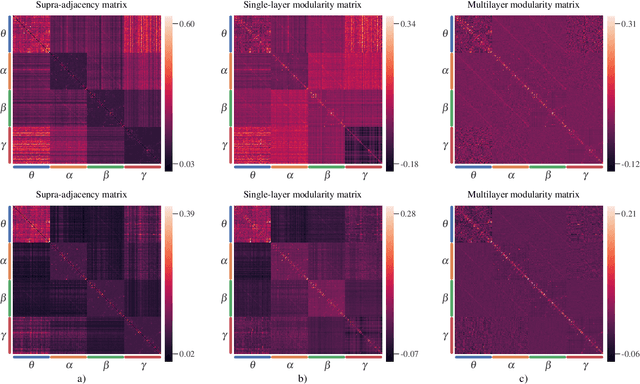
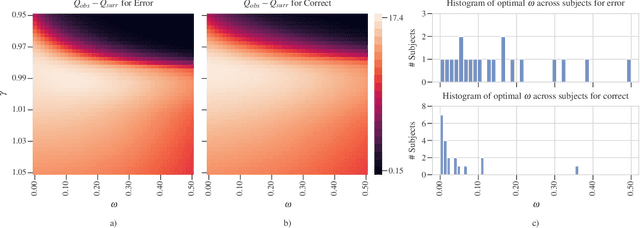
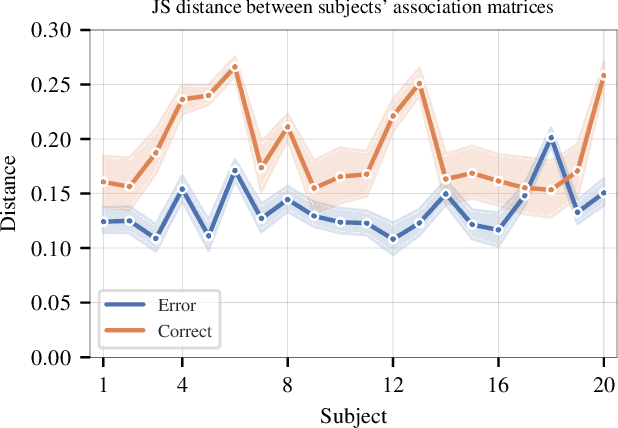
Objective: In recent years, the functional connectivity of the human brain has been studied with graph theoretical tools. One such approach is community detection which is fundamental for uncovering the localized networks. Existing methods focus on networks constructed from a single frequency band while ignoring multi-frequency nature of functional connectivity. Therefore, there is a need to study multi-frequency functional connectivity to be able to capture the full view of neuronal connectivity. Methods: In this paper, we use multilayer networks to model multi-frequency functional connectivity. In the proposed model, each layer corresponds to a different frequency band. We then extend the definition of modularity to multilayer networks to develop a new community detection algorithm. Results} The proposed approach is applied to electroencephalogram data collected during a study of error monitoring in the human brain. The differences between the community structures within and across different frequency bands for two response types, i.e. error and correct, are studied. Conclusion: The results indicate that following an error response, the brain organizes itself to form communities across frequencies, in particular between theta and gamma bands while a similar cross-frequency community formation is not observed for the correct response. Moreover, the community structures detected for the error response were more consistent across subjects compared to the community structures for correct response. Significance: The multi-frequency functional connectivity network models combined with multilayer community detection algorithms can reveal changes in cross-frequency functional connectivity network formation across different tasks and response types.

Community detection in multiplex networks based on orthogonal nonnegative matrix tri-factorization

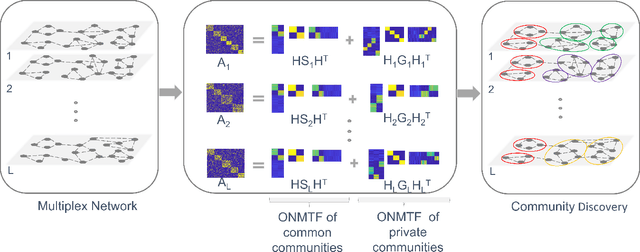
Networks provide a powerful tool to model complex systems where the different entities in the system are presented by nodes and their interactions by edges. Recently, there has been a growing interest in multiplex networks as they can represent the interactions between a pair of nodes through multiple types of links, each reflecting a distinct type of interaction. One of the important tools in understanding network topology is community detection. Although there are numerous works on community detection in single layer networks, existing work on multiplex community detection mostly focuses on learning a common community structure across layers without taking the heterogeneity of the different layers into account. In this paper, we introduce a new multiplex community detection approach that can identify communities that are common across layers as well as those that are unique to each layer. The proposed algorithm employs Orthogonal Nonnegative Matrix Tri-Factorization to model each layer's adjacency matrix as the sum of two low-rank matrix factorizations, corresponding to the common and private communities, respectively. The proposed algorithm is evaluated on both synthetic and real multiplex networks and compared to state-of-the-art techniques.