Community detection in multiplex networks based on orthogonal nonnegative matrix tri-factorization
Paper and Code
May 02, 2022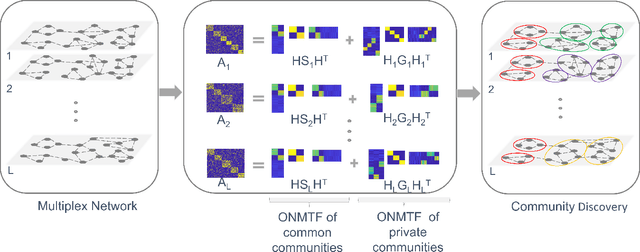


Networks provide a powerful tool to model complex systems where the different entities in the system are presented by nodes and their interactions by edges. Recently, there has been a growing interest in multiplex networks as they can represent the interactions between a pair of nodes through multiple types of links, each reflecting a distinct type of interaction. One of the important tools in understanding network topology is community detection. Although there are numerous works on community detection in single layer networks, existing work on multiplex community detection mostly focuses on learning a common community structure across layers without taking the heterogeneity of the different layers into account. In this paper, we introduce a new multiplex community detection approach that can identify communities that are common across layers as well as those that are unique to each layer. The proposed algorithm employs Orthogonal Nonnegative Matrix Tri-Factorization to model each layer's adjacency matrix as the sum of two low-rank matrix factorizations, corresponding to the common and private communities, respectively. The proposed algorithm is evaluated on both synthetic and real multiplex networks and compared to state-of-the-art techniques.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge