Learning Graph Filters for Structure-Function Coupling based Hub Node Identification

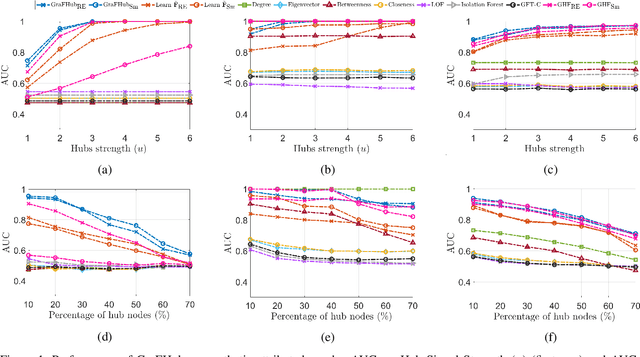
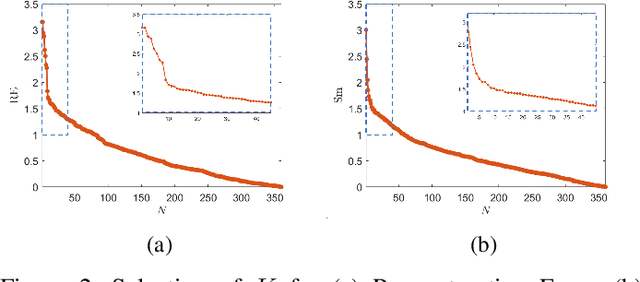
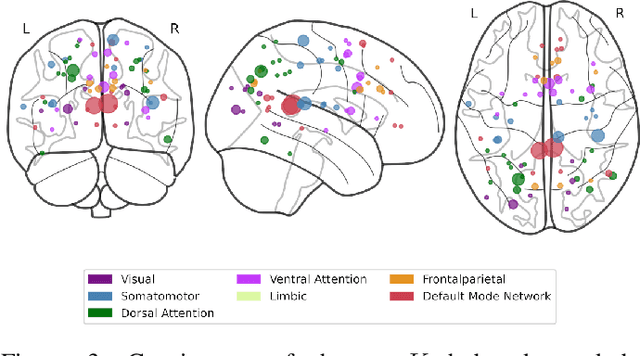
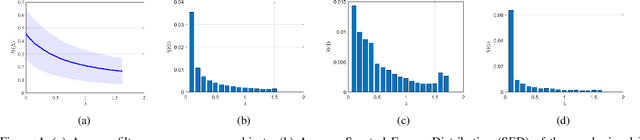
Over the past two decades, tools from network science have been leveraged to characterize the organization of both structural and functional networks of the brain. One such measure of network organization is hub node identification. Hubs are specialized nodes within a network that link distinct brain units corresponding to specialized functional processes. Conventional methods for identifying hub nodes utilize different types of centrality measures and participation coefficient to profile various aspects of nodal importance. These methods solely rely on the functional connectivity networks constructed from functional magnetic resonance imaging (fMRI), ignoring the structure-function coupling in the brain. In this paper, we introduce a graph signal processing (GSP) based hub detection framework that utilizes both the structural connectivity and the functional activation to identify hub nodes. The proposed framework models functional activity as graph signals on the structural connectivity. Hub nodes are then detected based on the premise that hub nodes are sparse, have higher level of activity compared to their neighbors, and the non-hub nodes' activity can be modeled as the output of a graph-based filter. Based on these assumptions, an optimization framework, GraFHub, is formulated to learn the coefficients of the optimal polynomial graph filter and detect the hub nodes. The proposed framework is evaluated on both simulated data and resting state fMRI (rs-fMRI) data from Human Connectome Project (HCP).

Multiview Graph Learning with Consensus Graph

Graph topology inference, i.e., learning graphs from a given set of nodal observations, is a significant task in many application domains. Existing approaches are mostly limited to learning a single graph assuming that the observed data is homogeneous. This is problematic because many modern datasets are heterogeneous or mixed and involve multiple related graphs, i.e., multiview graphs. Recent work proposing to learn multiview graphs ensures the similarity of learned view graphs through pairwise regularization, where each pair of views is encouraged to have similar structures. However, this approach cannot infer the shared structure across views. In this work, we propose an alternative method based on consensus regularization, where views are ensured to be similar through a learned consensus graph representing the common structure of the views. In particular, we propose an optimization problem, where graph data is assumed to be smooth over the multiview graph and the topology of the individual views and that of the consensus graph are learned, simultaneously. Our optimization problem is designed to be general in the sense that different regularization functions can be used depending on what the shared structure across views is. Moreover, we propose two regularization functions that extend fused and group graphical lasso to consensus based regularization. Proposed multiview graph learning is evaluated on simulated data and shown to have better performance than existing methods. It is also employed to infer the functional brain connectivity networks of multiple subjects from their electroencephalogram (EEG) recordings. The proposed method reveals the structure shared by subjects as well as the characteristics unique to each subject.

Community Detection in Multi-frequency EEG Networks

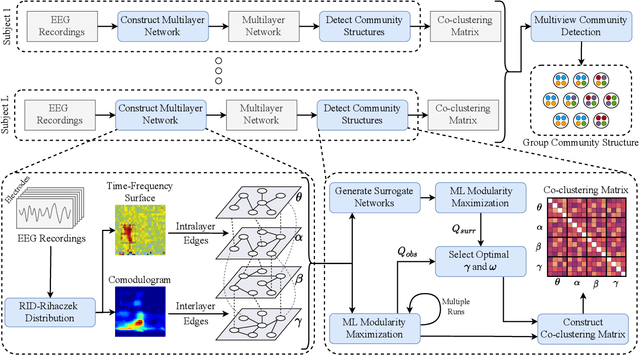
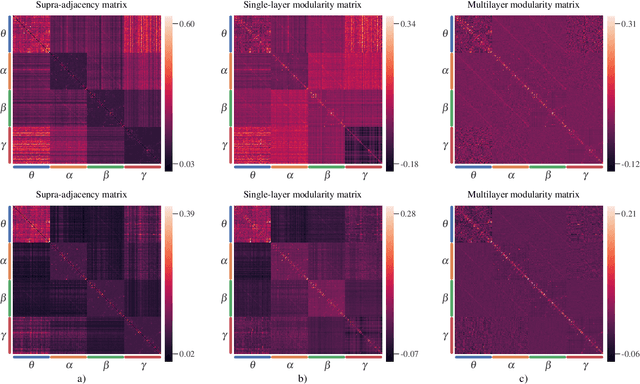
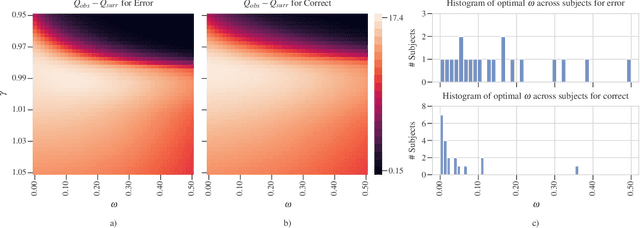
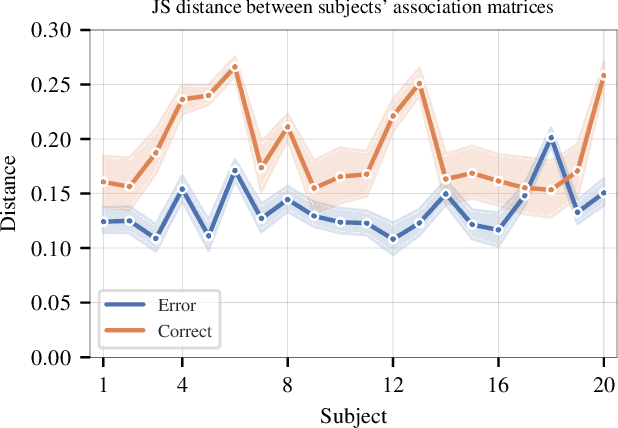
Objective: In recent years, the functional connectivity of the human brain has been studied with graph theoretical tools. One such approach is community detection which is fundamental for uncovering the localized networks. Existing methods focus on networks constructed from a single frequency band while ignoring multi-frequency nature of functional connectivity. Therefore, there is a need to study multi-frequency functional connectivity to be able to capture the full view of neuronal connectivity. Methods: In this paper, we use multilayer networks to model multi-frequency functional connectivity. In the proposed model, each layer corresponds to a different frequency band. We then extend the definition of modularity to multilayer networks to develop a new community detection algorithm. Results} The proposed approach is applied to electroencephalogram data collected during a study of error monitoring in the human brain. The differences between the community structures within and across different frequency bands for two response types, i.e. error and correct, are studied. Conclusion: The results indicate that following an error response, the brain organizes itself to form communities across frequencies, in particular between theta and gamma bands while a similar cross-frequency community formation is not observed for the correct response. Moreover, the community structures detected for the error response were more consistent across subjects compared to the community structures for correct response. Significance: The multi-frequency functional connectivity network models combined with multilayer community detection algorithms can reveal changes in cross-frequency functional connectivity network formation across different tasks and response types.