Unsupervised Total Variation Loss for Semi-supervised Deep Learning of Semantic Segmentation

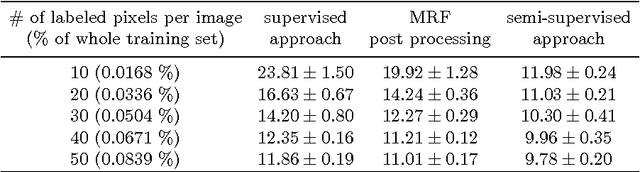
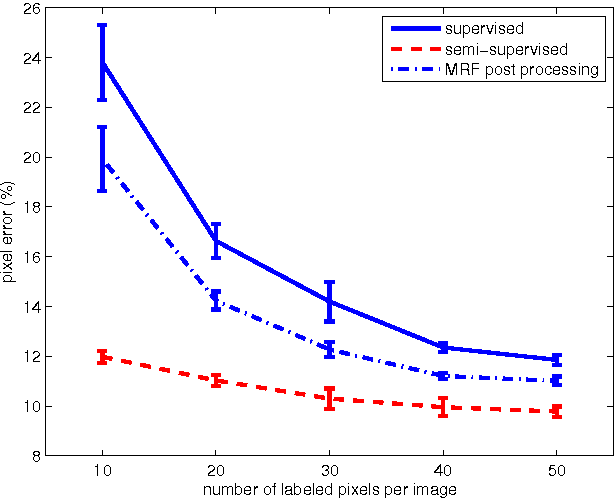
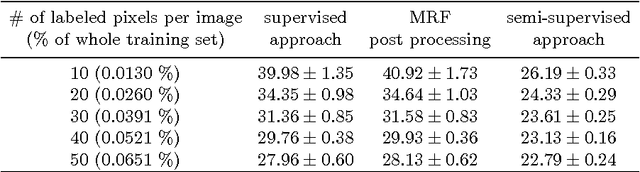
We introduce a novel unsupervised loss function for learning semantic segmentation with deep convolutional neural nets (ConvNet) when densely labeled training images are not available. More specifically, the proposed loss function penalizes the L1-norm of the gradient of the label probability vector image , i.e. total variation, produced by the ConvNet. This can be seen as a regularization term that promotes piecewise smoothness of the label probability vector image produced by the ConvNet during learning. The unsupervised loss function is combined with a supervised loss in a semi-supervised setting to learn ConvNets that can achieve high semantic segmentation accuracy even when only a tiny percentage of the pixels in the training images are labeled. We demonstrate significant improvements over the purely supervised setting in the Weizmann horse, Stanford background and Sift Flow datasets. Furthermore, we show that using the proposed piecewise smoothness constraint in the learning phase significantly outperforms post-processing results from a purely supervised approach with Markov Random Fields (MRF). Finally, we note that the framework we introduce is general and can be used to learn to label other types of structures such as curvilinear structures by modifying the unsupervised loss function accordingly.

Appearance invariance in convolutional networks with neighborhood similarity

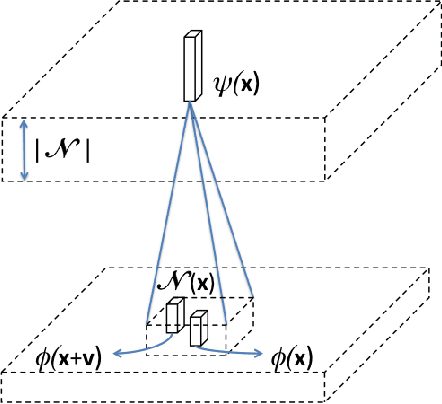
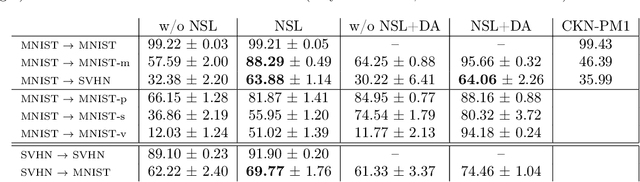
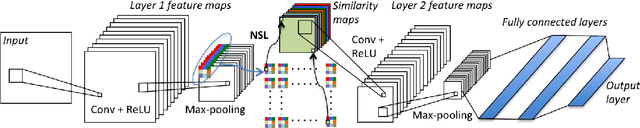
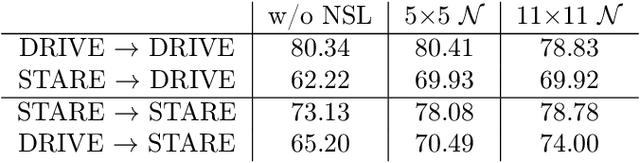
We present a neighborhood similarity layer (NSL) which induces appearance invariance in a network when used in conjunction with convolutional layers. We are motivated by the observation that, even though convolutional networks have low generalization error, their generalization capability does not extend to samples which are not represented by the training data. For instance, while novel appearances of learned concepts pose no problem for the human visual system, feedforward convolutional networks are generally not successful in such situations. Motivated by the Gestalt principle of grouping with respect to similarity, the proposed NSL transforms its input feature map using the feature vectors at each pixel as a frame of reference, i.e. center of attention, for its surrounding neighborhood. This transformation is spatially varying, hence not a convolution. It is differentiable; therefore, networks including the proposed layer can be trained in an end-to-end manner. We analyze the invariance of NSL to significant changes in appearance that are not represented in the training data. We also demonstrate its advantages for digit recognition, semantic labeling and cell detection problems.

Regularization With Stochastic Transformations and Perturbations for Deep Semi-Supervised Learning

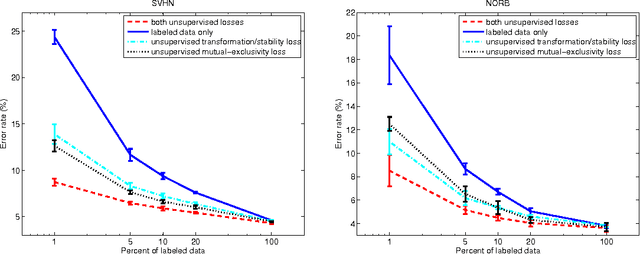
Effective convolutional neural networks are trained on large sets of labeled data. However, creating large labeled datasets is a very costly and time-consuming task. Semi-supervised learning uses unlabeled data to train a model with higher accuracy when there is a limited set of labeled data available. In this paper, we consider the problem of semi-supervised learning with convolutional neural networks. Techniques such as randomized data augmentation, dropout and random max-pooling provide better generalization and stability for classifiers that are trained using gradient descent. Multiple passes of an individual sample through the network might lead to different predictions due to the non-deterministic behavior of these techniques. We propose an unsupervised loss function that takes advantage of the stochastic nature of these methods and minimizes the difference between the predictions of multiple passes of a training sample through the network. We evaluate the proposed method on several benchmark datasets.

Mutual Exclusivity Loss for Semi-Supervised Deep Learning

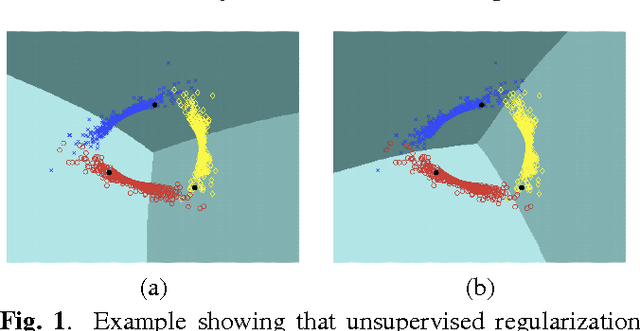
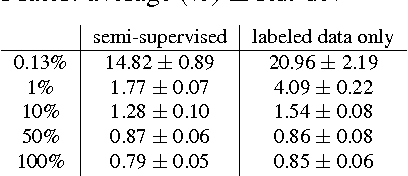
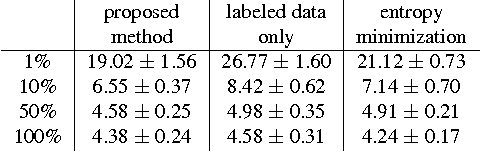
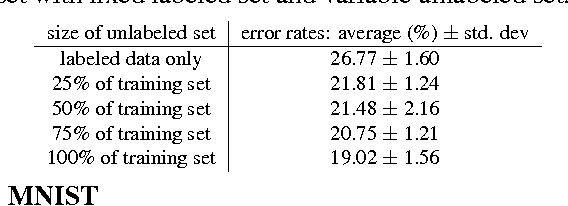
In this paper we consider the problem of semi-supervised learning with deep Convolutional Neural Networks (ConvNets). Semi-supervised learning is motivated on the observation that unlabeled data is cheap and can be used to improve the accuracy of classifiers. In this paper we propose an unsupervised regularization term that explicitly forces the classifier's prediction for multiple classes to be mutually-exclusive and effectively guides the decision boundary to lie on the low density space between the manifolds corresponding to different classes of data. Our proposed approach is general and can be used with any backpropagation-based learning method. We show through different experiments that our method can improve the object recognition performance of ConvNets using unlabeled data.

Disjunctive Normal Networks

Artificial neural networks are powerful pattern classifiers; however, they have been surpassed in accuracy by methods such as support vector machines and random forests that are also easier to use and faster to train. Backpropagation, which is used to train artificial neural networks, suffers from the herd effect problem which leads to long training times and limit classification accuracy. We use the disjunctive normal form and approximate the boolean conjunction operations with products to construct a novel network architecture. The proposed model can be trained by minimizing an error function and it allows an effective and intuitive initialization which solves the herd-effect problem associated with backpropagation. This leads to state-of-the art classification accuracy and fast training times. In addition, our model can be jointly optimized with convolutional features in an unified structure leading to state-of-the-art results on computer vision problems with fast convergence rates. A GPU implementation of LDNN with optional convolutional features is also available