Unsupervised Total Variation Loss for Semi-supervised Deep Learning of Semantic Segmentation
Paper and Code
Aug 07, 2018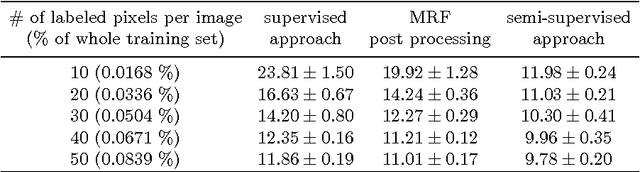
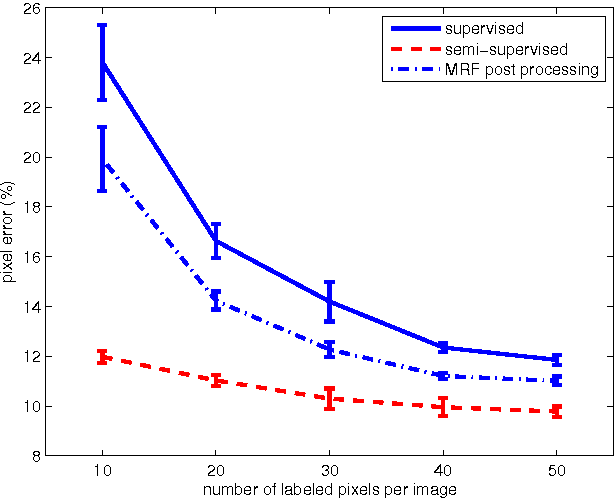

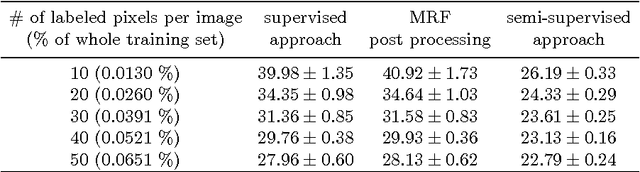
We introduce a novel unsupervised loss function for learning semantic segmentation with deep convolutional neural nets (ConvNet) when densely labeled training images are not available. More specifically, the proposed loss function penalizes the L1-norm of the gradient of the label probability vector image , i.e. total variation, produced by the ConvNet. This can be seen as a regularization term that promotes piecewise smoothness of the label probability vector image produced by the ConvNet during learning. The unsupervised loss function is combined with a supervised loss in a semi-supervised setting to learn ConvNets that can achieve high semantic segmentation accuracy even when only a tiny percentage of the pixels in the training images are labeled. We demonstrate significant improvements over the purely supervised setting in the Weizmann horse, Stanford background and Sift Flow datasets. Furthermore, we show that using the proposed piecewise smoothness constraint in the learning phase significantly outperforms post-processing results from a purely supervised approach with Markov Random Fields (MRF). Finally, we note that the framework we introduce is general and can be used to learn to label other types of structures such as curvilinear structures by modifying the unsupervised loss function accordingly.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge