Trajectory Tracking for Multi-Manipulator Systems in Constrained Environments

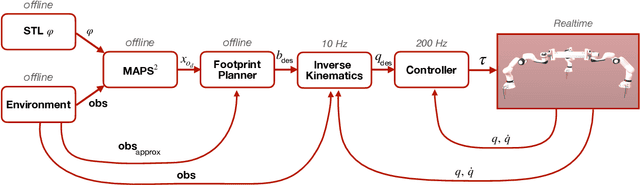
We consider the problem of cooperative manipulation by a mobile multi-manipulator system operating in obstacle-cluttered and highly constrained environments under spatio-temporal task specifications. The task requires transporting a grasped object while respecting both continuous robot dynamics and discrete geometric constraints arising from obstacles and narrow passages. To address this hybrid structure, we propose a multi-rate planning and control framework that combines offline generation of an STL-satisfying object trajectory and collision-free base footprints with online constrained inverse kinematics and continuous-time feedback control. The resulting closed-loop system enables coordinated reconfiguration of multiple manipulators while tracking the desired object motion. The approach is evaluated in high-fidelity physics simulations using three Franka Emika Panda mobile manipulators rigidly grasping an object.

Generating and Optimizing Topologically Distinct Guesses for Mobile Manipulator Path Planning

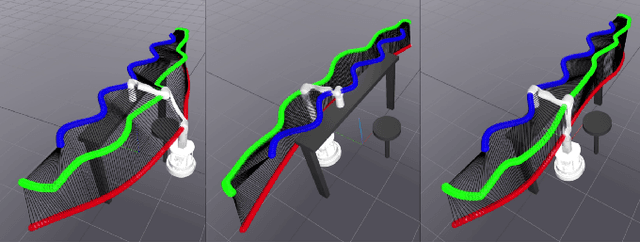
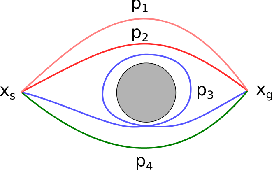
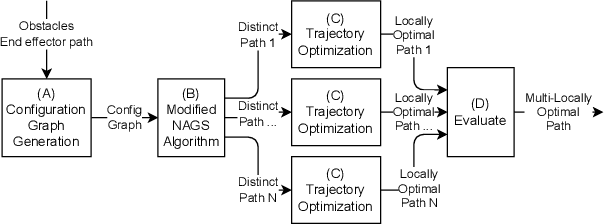
Optimal path planning often suffers from getting stuck in a local optimum. This is often the case for mobile manipulators due to nonconvexities induced by obstacles and robot kinematics. This paper attempts to circumvent this issue by proposing a pipeline to obtain multiple distinct local optima. By evaluating and selecting the optimum among multiple distinct local optima, it is likely to obtain a closer approximation of the global optimum. We demonstrate this capability in optimal path planning of nonholonomic mobile manipulators in the presence of obstacles and subject to end effector path constraints. The nonholomicity, obstacles, and end effector path constraints often cause direct optimal path planning approaches to get stuck in local optima. We demonstrate that our pipeline is able to circumvent this issue and produce a final local optimum that is close to the global optimum.

MAPS$^2$: Multi-Robot Anytime Motion Planning under Signal Temporal Logic Specifications

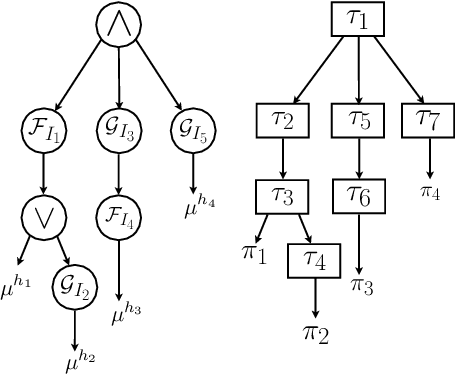
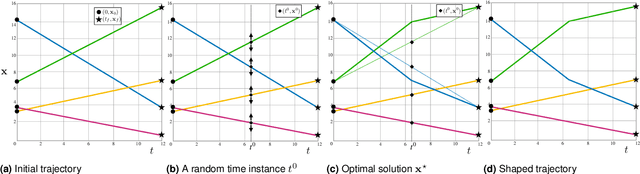
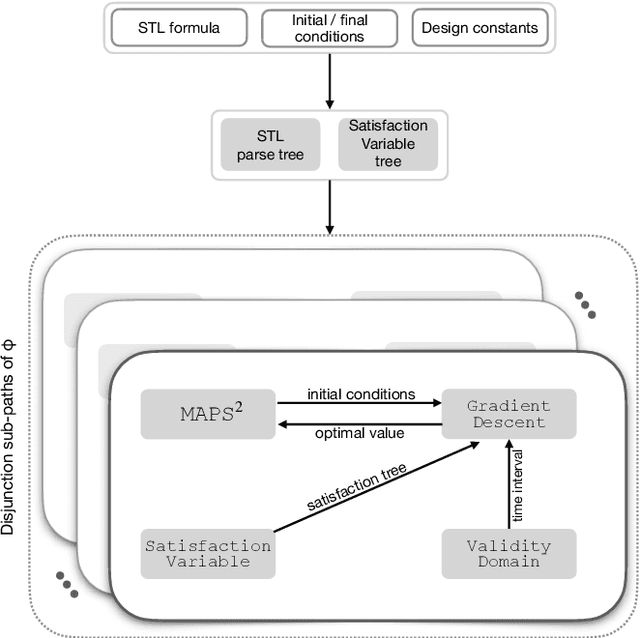
This article presents MAPS$^2$ : a distributed algorithm that allows multi-robot systems to deliver coupled tasks expressed as Signal Temporal Logic (STL) constraints. Classical control theoretical tools addressing STL constraints either adopt a limited fragment of the STL formula or require approximations of min/max operators, whereas works maximising robustness through optimisation-based methods often suffer from local minima, relaxing any completeness arguments due to the NP-hard nature of the problem. Endowed with probabilistic guarantees, MAPS$^2$ provides an anytime algorithm that iteratively improves the robots' trajectories. The algorithm selectively imposes spatial constraints by taking advantage of the temporal properties of the STL. The algorithm is distributed, in the sense that each robot calculates its trajectory by communicating only with its immediate neighbours as defined via a communication graph. We illustrate the efficiency of MAPS$^2$ by conducting extensive simulation and experimental studies, verifying the generation of STL satisfying trajectories.