Decoupled Design of Time-Varying Control Barrier Functions via Equivariances

This article presents a systematic method for designing time-varying Control Barrier Functions (CBF) composed of a time-invariant component and multiple time-dependent components, leveraging structural properties of the system dynamics. The method involves the construction of a specific class of time-invariant CBFs that encode the system's dynamic capabilities with respect to a given constraint, and augments them subsequently with appropriately designed time-dependent transformations. While transformations uniformly varying the time-invariant CBF can be applied to arbitrary systems, transformations exploiting structural properties in the dynamics - equivariances in particular - enable the handling of a broader and more expressive class of time-varying constraints. The article shows how to leverage such properties in the design of time-varying CBFs. The proposed method decouples the design of time variations from the computationally expensive construction of the underlying CBFs, thereby providing a computationally attractive method to the design of time-varying CBFs. The method accounts for input constraints and under-actuation, and requires only qualitative knowledge on the time-variation of the constraints making it suitable to the application in uncertain environments.

Leveraging Equivariances and Symmetries in the Control Barrier Function Synthesis

The synthesis of Control Barrier Functions (CBFs) often involves demanding computations or a meticulous construction. However, structural properties of the system dynamics and constraints have the potential to mitigate these challenges. In this paper, we explore how equivariances in the dynamics, loosely speaking a form of symmetry, can be leveraged in the CBF synthesis. Although CBFs are generally not inherently symmetric, we show how equivariances in the dynamics and symmetries in the constraints induce symmetries in CBFs derived through reachability analysis. This insight allows us to infer their CBF values across the entire domain from their values on a subset, leading to significant computational savings. Interestingly, equivariances can be even leveraged to the CBF synthesis for non-symmetric constraints. Specifically, we show how a partially known CBF can be leveraged together with equivariances to construct a CBF for various new constraints. Throughout the paper, we provide examples illustrating the theoretical findings. Furthermore, a numerical study investigates the computational gains from invoking equivariances into the CBF synthesis.

Generating and Optimizing Topologically Distinct Guesses for Mobile Manipulator Path Planning

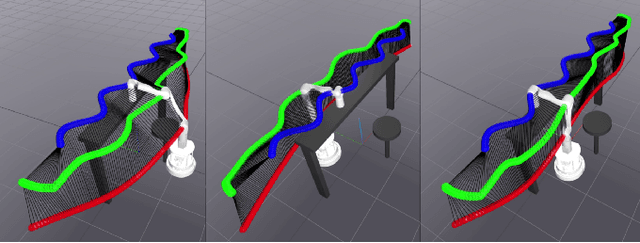
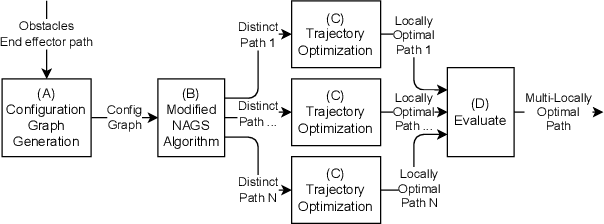
Optimal path planning often suffers from getting stuck in a local optimum. This is often the case for mobile manipulators due to nonconvexities induced by obstacles and robot kinematics. This paper attempts to circumvent this issue by proposing a pipeline to obtain multiple distinct local optima. By evaluating and selecting the optimum among multiple distinct local optima, it is likely to obtain a closer approximation of the global optimum. We demonstrate this capability in optimal path planning of nonholonomic mobile manipulators in the presence of obstacles and subject to end effector path constraints. The nonholomicity, obstacles, and end effector path constraints often cause direct optimal path planning approaches to get stuck in local optima. We demonstrate that our pipeline is able to circumvent this issue and produce a final local optimum that is close to the global optimum.