Quantum Inverse Fast Fourier Transform

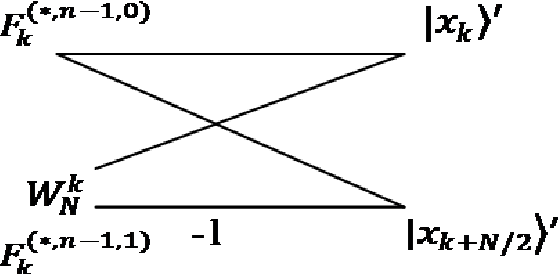
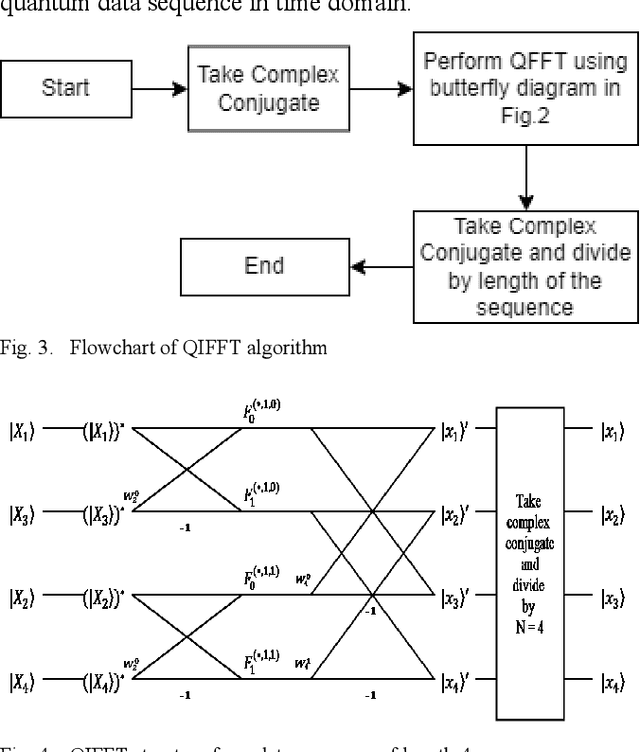
In this paper, an algorithm for Quantum Inverse Fast Fourier Transform (QIFFT) is developed to work for quantum data. Analogous to a classical discrete signal, a quantum signal can be represented in Dirac notation, application of QIFFT is a tensor transformation from frequency domain to time domain. If the tensors are merely complex entries, then we get the classical scenario. We have included the complete formulation of QIFFT algorithm from the classical model and have included butterfly diagram. QIFFT outperforms regular inversion of Quantum Fourier Transform (QFT) in terms of computational complexity, quantum parallelism and improved versatility.

Physics-guided Loss Functions Improve Deep Learning Performance in Inverse Scattering

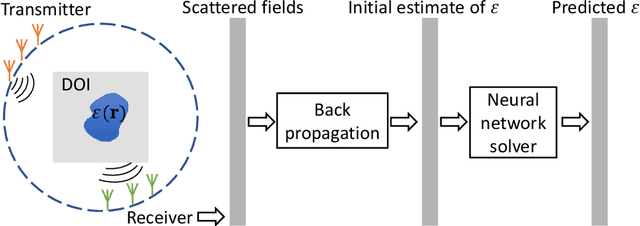
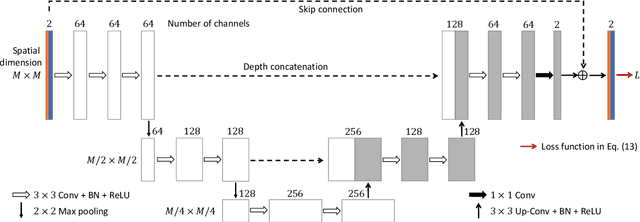
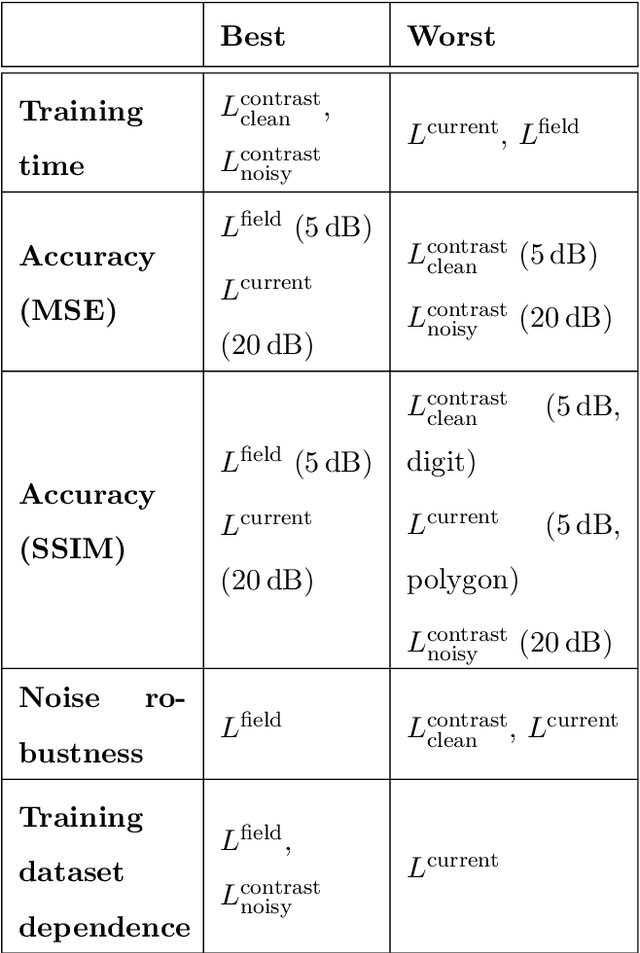
Solving electromagnetic inverse scattering problems (ISPs) is challenging due to the intrinsic nonlinearity, ill-posedness, and expensive computational cost. Recently, deep neural network (DNN) techniques have been successfully applied on ISPs and shown potential of superior imaging over conventional methods. In this paper, we analyse the analogy between DNN solvers and traditional iterative algorithms and discuss how important physical phenomena cannot be effectively incorporated in the training process. We show the importance of including near-field priors in the learning process of DNNs. To this end, we propose new designs of loss functions which incorporate multiple-scattering based near-field quantities (such as scattered fields or induced currents within domain of interest). Effects of physics-guided loss functions are studied using a variety of numerical experiments. Pros and cons of the investigated ISP solvers with different loss functions are summarized.