Understanding the Impact of Evaluation Metrics in Kinetic Models for Consensus-based Segmentation

In this article we extend a recently introduced kinetic model for consensus-based segmentation of images. In particular, we will interpret the set of pixels of a 2D image as an interacting particle system which evolves in time in view of a consensus-type process obtained by interactions between pixels and external noise. Thanks to a kinetic formulation of the introduced model we derive the large time solution of the model. We will show that the choice of parameters defining the segmentation task can be chosen from a plurality of loss functions characterising the evaluation metrics.

A kinetic approach to consensus-based segmentation of biomedical images

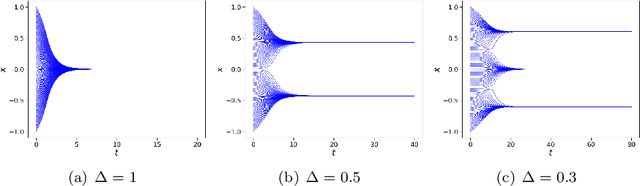
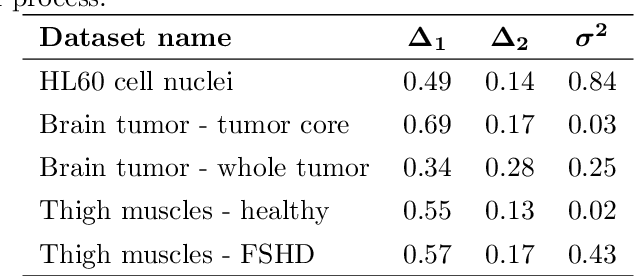
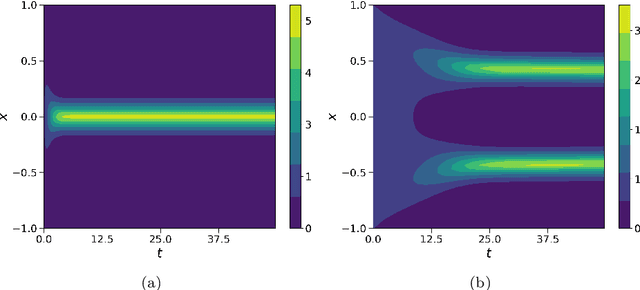
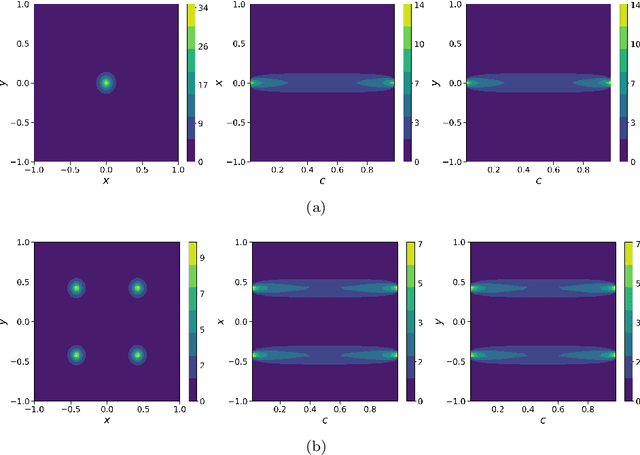
In this work, we apply a kinetic version of a bounded confidence consensus model to biomedical segmentation problems. In the presented approach, time-dependent information on the microscopic state of each particle/pixel includes its space position and a feature representing a static characteristic of the system, i.e. the gray level of each pixel. From the introduced microscopic model we derive a kinetic formulation of the model. The large time behavior of the system is then computed with the aid of a surrogate Fokker-Planck approach that can be obtained in the quasi-invariant scaling. We exploit the computational efficiency of direct simulation Monte Carlo methods for the obtained Boltzmann-type description of the problem for parameter identification tasks. Based on a suitable loss function measuring the distance between the ground truth segmentation mask and the evaluated mask, we minimize the introduced segmentation metric for a relevant set of 2D gray-scale images. Applications to biomedical segmentation concentrate on different imaging research contexts.