Convergence and Optimality of Policy Gradient Methods in Weakly Smooth Settings

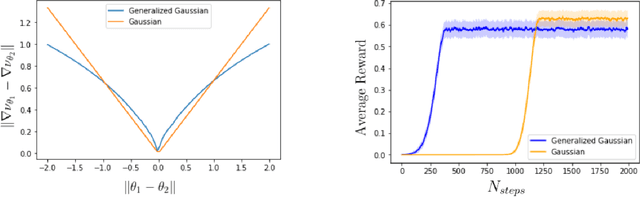
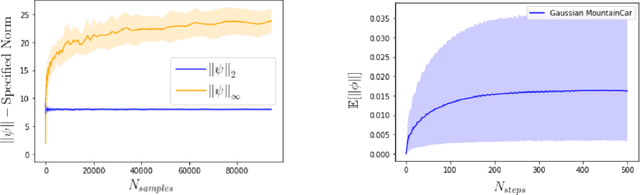
Policy gradient methods have been frequently applied to problems in control and reinforcement learning with great success, yet existing convergence analysis still relies on non-intuitive, impractical and often opaque conditions. In particular, existing rates are achieved in limited settings, under strict smoothness and bounded conditions. In this work, we establish explicit convergence rates of policy gradient methods without relying on these conditions, instead extending the convergence regime to weakly smooth policy classes with $L_2$ integrable gradient. We provide intuitive examples to illustrate the insight behind these new conditions. We also characterize the sufficiency conditions for the ergodicity of near-linear MDPs, which represent an important class of problems. Notably, our analysis also shows that fast convergence rates are achievable for both the standard policy gradient and the natural policy gradient algorithms under these assumptions. Lastly we provide conditions and analysis for optimality of the converged policies.

One-Shot Pruning of Recurrent Neural Networks by Jacobian Spectrum Evaluation

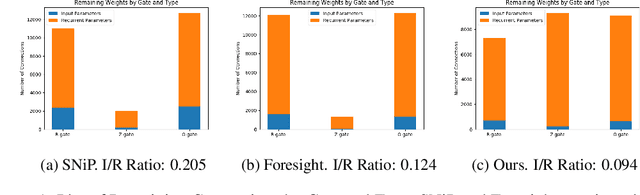
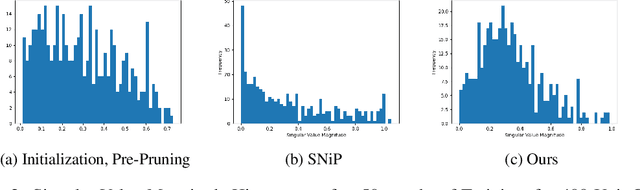
Recent advances in the sparse neural network literature have made it possible to prune many large feed forward and convolutional networks with only a small quantity of data. Yet, these same techniques often falter when applied to the problem of recovering sparse recurrent networks. These failures are quantitative: when pruned with recent techniques, RNNs typically obtain worse performance than they do under a simple random pruning scheme. The failures are also qualitative: the distribution of active weights in a pruned LSTM or GRU network tend to be concentrated in specific neurons and gates, and not well dispersed across the entire architecture. We seek to rectify both the quantitative and qualitative issues with recurrent network pruning by introducing a new recurrent pruning objective derived from the spectrum of the recurrent Jacobian. Our objective is data efficient (requiring only 64 data points to prune the network), easy to implement, and produces 95% sparse GRUs that significantly improve on existing baselines. We evaluate on sequential MNIST, Billion Words, and Wikitext.