Convergence and Optimality of Policy Gradient Methods in Weakly Smooth Settings

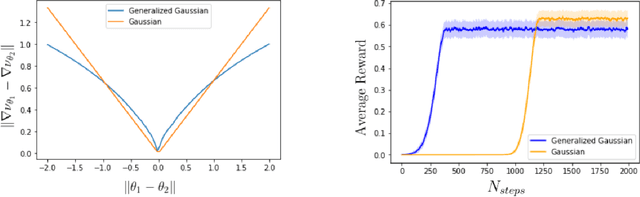
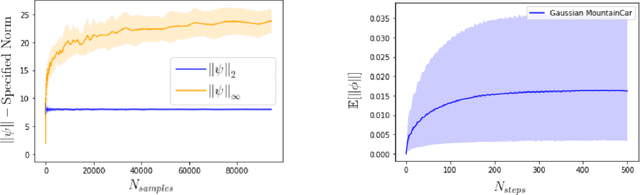
Policy gradient methods have been frequently applied to problems in control and reinforcement learning with great success, yet existing convergence analysis still relies on non-intuitive, impractical and often opaque conditions. In particular, existing rates are achieved in limited settings, under strict smoothness and bounded conditions. In this work, we establish explicit convergence rates of policy gradient methods without relying on these conditions, instead extending the convergence regime to weakly smooth policy classes with $L_2$ integrable gradient. We provide intuitive examples to illustrate the insight behind these new conditions. We also characterize the sufficiency conditions for the ergodicity of near-linear MDPs, which represent an important class of problems. Notably, our analysis also shows that fast convergence rates are achievable for both the standard policy gradient and the natural policy gradient algorithms under these assumptions. Lastly we provide conditions and analysis for optimality of the converged policies.