Predictive State Representations: A New Theory for Modeling Dynamical Systems

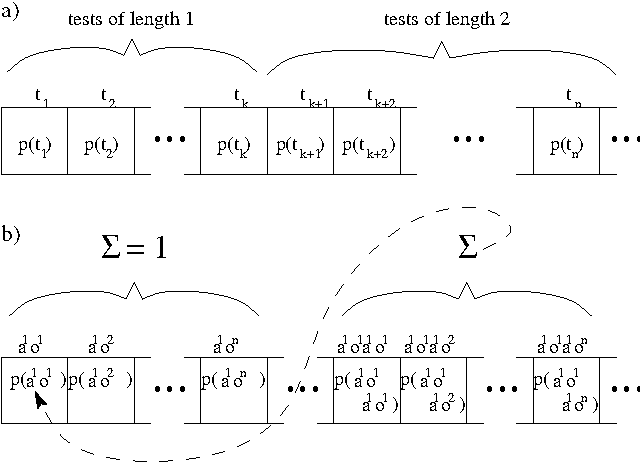
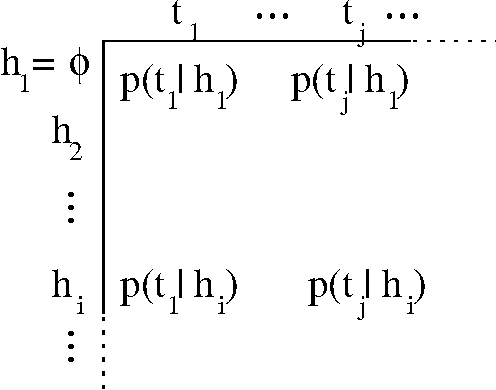
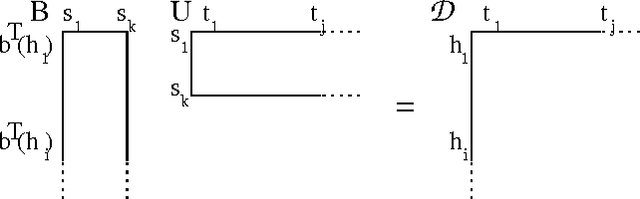
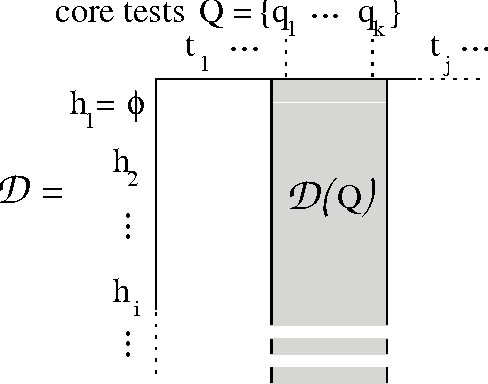
Modeling dynamical systems, both for control purposes and to make predictions about their behavior, is ubiquitous in science and engineering. Predictive state representations (PSRs) are a recently introduced class of models for discrete-time dynamical systems. The key idea behind PSRs and the closely related OOMs (Jaeger's observable operator models) is to represent the state of the system as a set of predictions of observable outcomes of experiments one can do in the system. This makes PSRs rather different from history-based models such as nth-order Markov models and hidden-state-based models such as HMMs and POMDPs. We introduce an interesting construct, the systemdynamics matrix, and show how PSRs can be derived simply from it. We also use this construct to show formally that PSRs are more general than both nth-order Markov models and HMMs/POMDPs. Finally, we discuss the main difference between PSRs and OOMs and conclude with directions for future work.

Predictive Linear-Gaussian Models of Stochastic Dynamical Systems

Models of dynamical systems based on predictive state representations (PSRs) are defined strictly in terms of observable quantities, in contrast with traditional models (such as Hidden Markov Models) that use latent variables or statespace representations. In addition, PSRs have an effectively infinite memory, allowing them to model some systems that finite memory-based models cannot. Thus far, PSR models have primarily been developed for domains with discrete observations. Here, we develop the Predictive Linear-Gaussian (PLG) model, a class of PSR models for domains with continuous observations. We show that PLG models subsume Linear Dynamical System models (also called Kalman filter models or state-space models) while using fewer parameters. We also introduce an algorithm to estimate PLG parameters from data, and contrast it with standard Expectation Maximization (EM) algorithms used to estimate Kalman filter parameters. We show that our algorithm is a consistent estimation procedure and present preliminary empirical results suggesting that our algorithm outperforms EM, particularly as the model dimension increases.