Predictive State Representations: A New Theory for Modeling Dynamical Systems
Paper and Code
Jul 11, 2012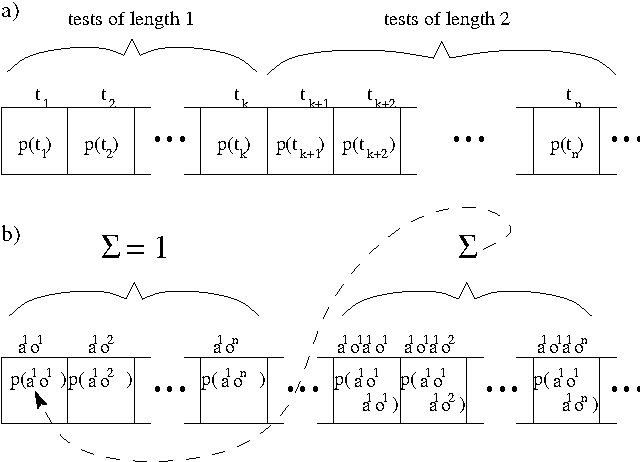
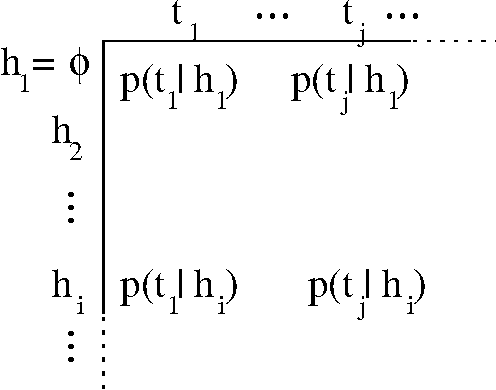
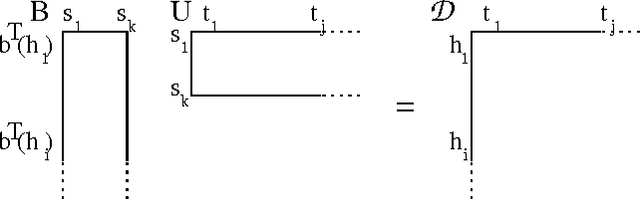
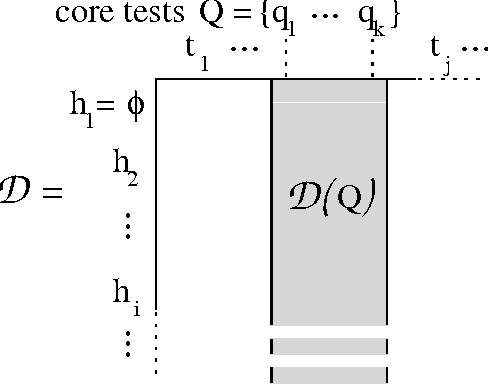
Modeling dynamical systems, both for control purposes and to make predictions about their behavior, is ubiquitous in science and engineering. Predictive state representations (PSRs) are a recently introduced class of models for discrete-time dynamical systems. The key idea behind PSRs and the closely related OOMs (Jaeger's observable operator models) is to represent the state of the system as a set of predictions of observable outcomes of experiments one can do in the system. This makes PSRs rather different from history-based models such as nth-order Markov models and hidden-state-based models such as HMMs and POMDPs. We introduce an interesting construct, the systemdynamics matrix, and show how PSRs can be derived simply from it. We also use this construct to show formally that PSRs are more general than both nth-order Markov models and HMMs/POMDPs. Finally, we discuss the main difference between PSRs and OOMs and conclude with directions for future work.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge