Development of a dynamic type 2 diabetes risk prediction tool: a UK Biobank study

Diabetes affects over 400 million people and is among the leading causes of morbidity worldwide. Identification of high-risk individuals can support early diagnosis and prevention of disease development through lifestyle changes. However, the majority of existing risk scores require information about blood-based factors which are not obtainable outside of the clinic. Here, we aimed to develop an accessible solution that could be deployed digitally and at scale. We developed a predictive 10-year type 2 diabetes risk score using 301 features derived from 472,830 participants in the UK Biobank dataset while excluding any features which are not easily obtainable by a smartphone. Using a data-driven feature selection process, 19 features were included in the final reduced model. A Cox proportional hazards model slightly overperformed a DeepSurv model trained using the same features, achieving a concordance index of 0.818 (95% CI: 0.812-0.823), compared to 0.811 (95% CI: 0.806-0.815). The final model showed good calibration. This tool can be used for clinical screening of individuals at risk of developing type 2 diabetes and to foster patient empowerment by broadening their knowledge of the factors affecting their personal risk.

Decoding Hidden Markov Models Faster Than Viterbi Via Online Matrix-Vector (max, +)-Multiplication

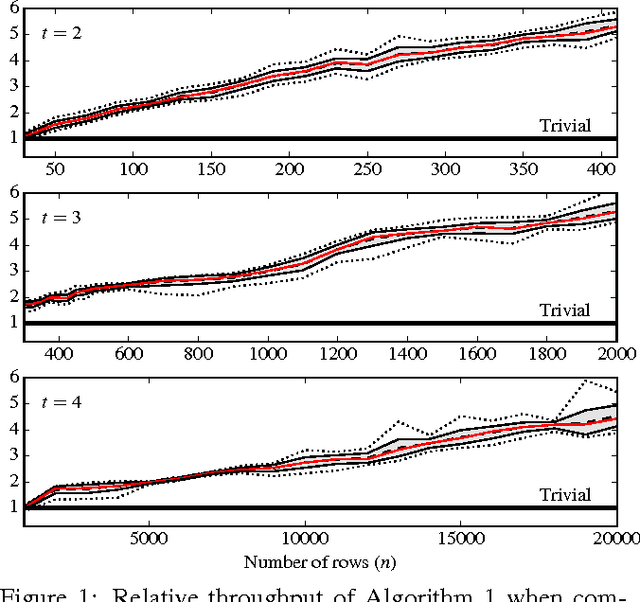
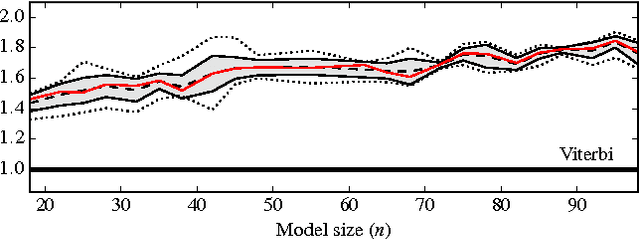
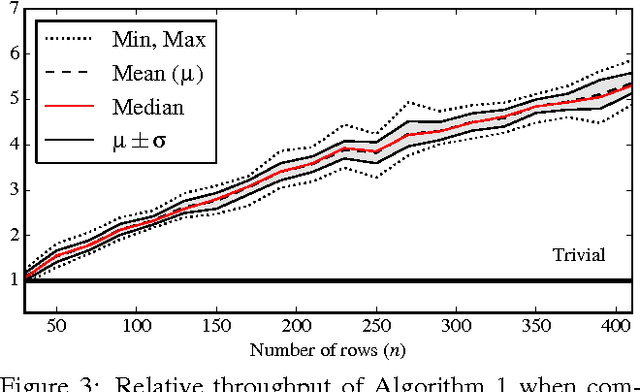
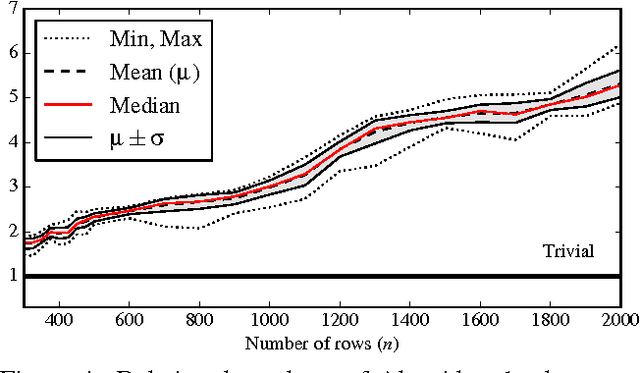
In this paper, we present a novel algorithm for the maximum a posteriori decoding (MAPD) of time-homogeneous Hidden Markov Models (HMM), improving the worst-case running time of the classical Viterbi algorithm by a logarithmic factor. In our approach, we interpret the Viterbi algorithm as a repeated computation of matrix-vector $(\max, +)$-multiplications. On time-homogeneous HMMs, this computation is online: a matrix, known in advance, has to be multiplied with several vectors revealed one at a time. Our main contribution is an algorithm solving this version of matrix-vector $(\max,+)$-multiplication in subquadratic time, by performing a polynomial preprocessing of the matrix. Employing this fast multiplication algorithm, we solve the MAPD problem in $O(mn^2/ \log n)$ time for any time-homogeneous HMM of size $n$ and observation sequence of length $m$, with an extra polynomial preprocessing cost negligible for $m > n$. To the best of our knowledge, this is the first algorithm for the MAPD problem requiring subquadratic time per observation, under the only assumption -- usually verified in practice -- that the transition probability matrix does not change with time.