MaryBeth Defrance
BiMi Sheets: Infosheets for bias mitigation methods
May 28, 2025
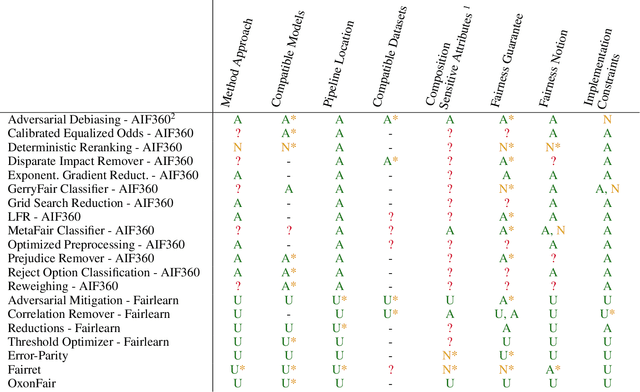
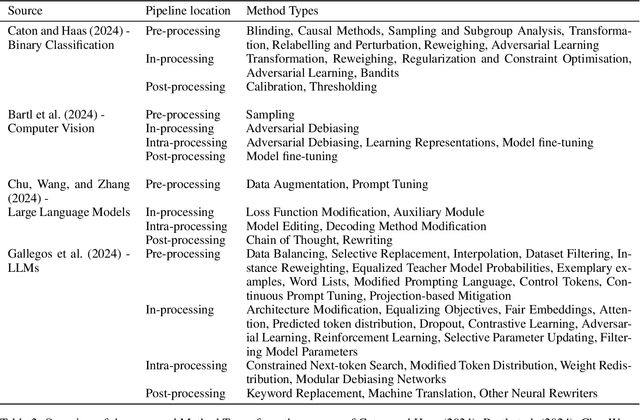

Abstract:Over the past 15 years, hundreds of bias mitigation methods have been proposed in the pursuit of fairness in machine learning (ML). However, algorithmic biases are domain-, task-, and model-specific, leading to a `portability trap': bias mitigation solutions in one context may not be appropriate in another. Thus, a myriad of design choices have to be made when creating a bias mitigation method, such as the formalization of fairness it pursues, and where and how it intervenes in the ML pipeline. This creates challenges in benchmarking and comparing the relative merits of different bias mitigation methods, and limits their uptake by practitioners. We propose BiMi Sheets as a portable, uniform guide to document the design choices of any bias mitigation method. This enables researchers and practitioners to quickly learn its main characteristics and to compare with their desiderata. Furthermore, the sheets' structure allow for the creation of a structured database of bias mitigation methods. In order to foster the sheets' adoption, we provide a platform for finding and creating BiMi Sheets at bimisheet.com.
Biased Heritage: How Datasets Shape Models in Facial Expression Recognition
Mar 05, 2025Abstract:In recent years, the rapid development of artificial intelligence (AI) systems has raised concerns about our ability to ensure their fairness, that is, how to avoid discrimination based on protected characteristics such as gender, race, or age. While algorithmic fairness is well-studied in simple binary classification tasks on tabular data, its application to complex, real-world scenarios-such as Facial Expression Recognition (FER)-remains underexplored. FER presents unique challenges: it is inherently multiclass, and biases emerge across intersecting demographic variables, each potentially comprising multiple protected groups. We present a comprehensive framework to analyze bias propagation from datasets to trained models in image-based FER systems, while introducing new bias metrics specifically designed for multiclass problems with multiple demographic groups. Our methodology studies bias propagation by (1) inducing controlled biases in FER datasets, (2) training models on these biased datasets, and (3) analyzing the correlation between dataset bias metrics and model fairness notions. Our findings reveal that stereotypical biases propagate more strongly to model predictions than representational biases, suggesting that preventing emotion-specific demographic patterns should be prioritized over general demographic balance in FER datasets. Additionally, we observe that biased datasets lead to reduced model accuracy, challenging the assumed fairness-accuracy trade-off.
ABCFair: an Adaptable Benchmark approach for Comparing Fairness Methods
Sep 25, 2024



Abstract:Numerous methods have been implemented that pursue fairness with respect to sensitive features by mitigating biases in machine learning. Yet, the problem settings that each method tackles vary significantly, including the stage of intervention, the composition of sensitive features, the fairness notion, and the distribution of the output. Even in binary classification, these subtle differences make it highly complicated to benchmark fairness methods, as their performance can strongly depend on exactly how the bias mitigation problem was originally framed. Hence, we introduce ABCFair, a benchmark approach which allows adapting to the desiderata of the real-world problem setting, enabling proper comparability between methods for any use case. We apply ABCFair to a range of pre-, in-, and postprocessing methods on both large-scale, traditional datasets and on a dual label (biased and unbiased) dataset to sidestep the fairness-accuracy trade-off.
fairret: a Framework for Differentiable Fairness Regularization Terms
Oct 26, 2023Abstract:Current tools for machine learning fairness only admit a limited range of fairness definitions and have seen little integration with automatic differentiation libraries, despite the central role these libraries play in modern machine learning pipelines. We introduce a framework of fairness regularization terms (fairrets) which quantify bias as modular objectives that are easily integrated in automatic differentiation pipelines. By employing a general definition of fairness in terms of linear-fractional statistics, a wide class of fairrets can be computed efficiently. Experiments show the behavior of their gradients and their utility in enforcing fairness with minimal loss of predictive power compared to baselines. Our contribution includes a PyTorch implementation of the fairret framework.
Maximal Fairness
Apr 12, 2023



Abstract:Fairness in AI has garnered quite some attention in research, and increasingly also in society. The so-called "Impossibility Theorem" has been one of the more striking research results with both theoretical and practical consequences, as it states that satisfying a certain combination of fairness measures is impossible. To date, this negative result has not yet been complemented with a positive one: a characterization of which combinations of fairness notions are possible. This work aims to fill this gap by identifying maximal sets of commonly used fairness measures that can be simultaneously satisfied. The fairness measures used are demographic parity, equal opportunity, false positive parity, predictive parity, predictive equality, overall accuracy equality and treatment equality. We conclude that in total 12 maximal sets of these fairness measures are possible, among which seven combinations of two measures, and five combinations of three measures. Our work raises interest questions regarding the practical relevance of each of these 12 maximal fairness notions in various scenarios.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge