Informed Circular Fields for Global Reactive Obstacle Avoidance of Robotic Manipulators

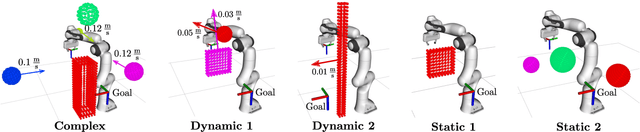
In this paper a global reactive motion planning framework for robotic manipulators in complex dynamic environments is presented. In particular, the circular field predictions (CFP) planner from Becker et al. (2021) is extended to ensure obstacle avoidance of the whole structure of a robotic manipulator. Towards this end, a motion planning framework is developed that leverages global information about promising avoidance directions from arbitrary configuration space motion planners, resulting in improved global trajectories while reactively avoiding dynamic obstacles and decreasing the required computational power. The resulting motion planning framework is tested in multiple simulations with complex and dynamic obstacles and demonstrates great potential compared to existing motion planning approaches.

Motion Planning using Reactive Circular Fields: A 2D Analysis of Collision Avoidance and Goal Convergence

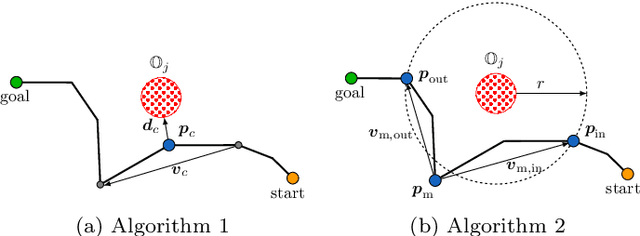
Recently, many reactive trajectory planning approaches were suggested in the literature because of their inherent immediate adaption in the ever more demanding cluttered and unpredictable environments of robotic systems. However, typically those approaches are only locally reactive without considering global path planning and no guarantees for simultaneous collision avoidance and goal convergence can be given. In this paper, we study a recently developed circular field (CF)-based motion planner that combines local reactive control with global trajectory generation by adapting an artificial magnetic field such that multiple trajectories around obstacles can be evaluated. In particular, we provide a mathematically rigorous analysis of this planner in a planar environment to ensure safe motion of the controlled robot. Contrary to existing results, the derived collision avoidance analysis covers the entire CF motion planning algorithm including attractive forces for goal convergence and is not limited to a specific choice of the rotation field, i.e., our guarantees are not limited to a specific potentially suboptimal trajectory. Our Lyapunov-type collision avoidance analysis is based on the definition of an (equivalent) two-dimensional auxiliary system, which enables us to provide tight, if and only if conditions for the case of a collision with point obstacles. Furthermore, we show how this analysis naturally extends to multiple obstacles and we specify sufficient conditions for goal convergence. Finally, we provide a challenging simulation scenario with multiple non-convex point cloud obstacles and demonstrate collision avoidance and goal convergence.