Martin von Kurnatowski
Capturing and incorporating expert knowledge into machine learning models for quality prediction in manufacturing
Feb 04, 2022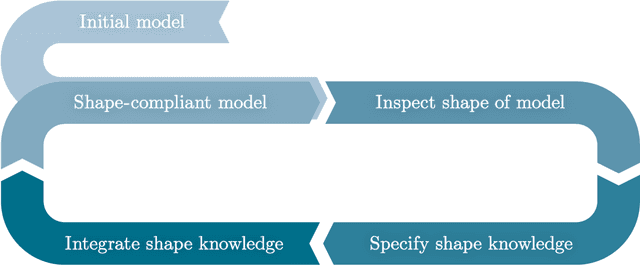

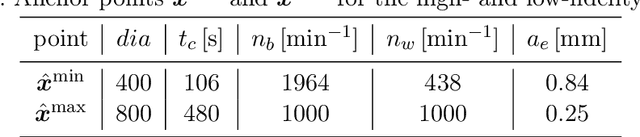
Abstract:Increasing digitalization enables the use of machine learning methods for analyzing and optimizing manufacturing processes. A main application of machine learning is the construction of quality prediction models, which can be used, among other things, for documentation purposes, as assistance systems for process operators, or for adaptive process control. The quality of such machine learning models typically strongly depends on the amount and the quality of data used for training. In manufacturing, the size of available datasets before start of production is often limited. In contrast to data, expert knowledge commonly is available in manufacturing. Therefore, this study introduces a general methodology for building quality prediction models with machine learning methods on small datasets by integrating shape expert knowledge, that is, prior knowledge about the shape of the input-output relationship to be learned. The proposed methodology is applied to a brushing process with $125$ data points for predicting the surface roughness as a function of five process variables. As opposed to conventional machine learning methods for small datasets, the proposed methodology produces prediction models that strictly comply with all the expert knowledge specified by the involved process specialists. In particular, the direct involvement of process experts in the training of the models leads to a very clear interpretation and, by extension, to a high acceptance of the models. Another merit of the proposed methodology is that, in contrast to most conventional machine learning methods, it involves no time-consuming and often heuristic hyperparameter tuning or model selection step.
Compensating data shortages in manufacturing with monotonicity knowledge
Oct 29, 2020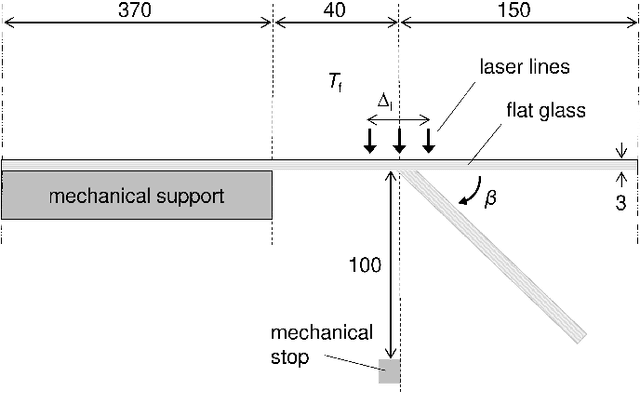

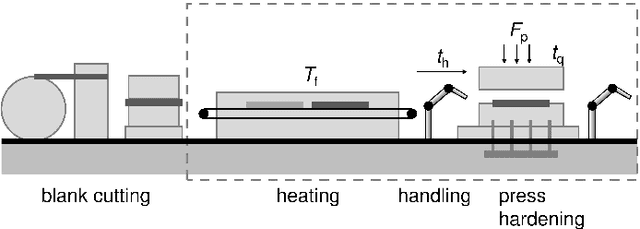
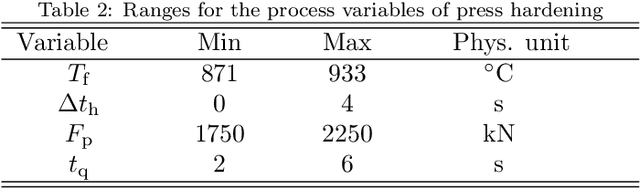
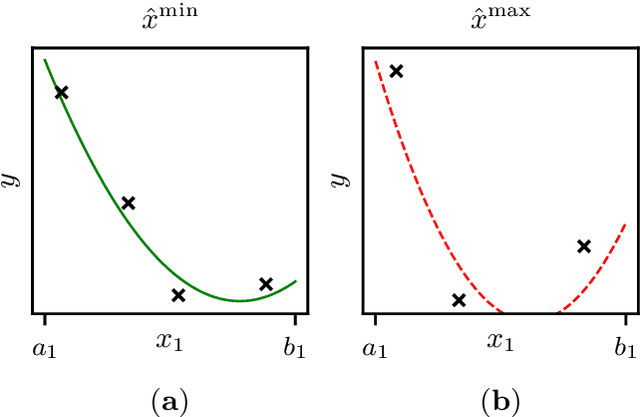
Abstract:We present a regression method for enhancing the predictive power of a model by exploiting expert knowledge in the form of shape constraints, or more specifically, monotonicity constraints. Incorporating such information is particularly useful when the available data sets are small or do not cover the entire input space, as is often the case in manufacturing applications. We set up the regression subject to the considered monotonicity constraints as a semi-infinite optimization problem, and we propose an adaptive solution algorithm. The method is conceptually simple, applicable in multiple dimensions and can be extended to more general shape constraints. It is tested and validated on two real-world manufacturing processes, namely laser glass bending and press hardening of sheet metal. It is found that the resulting models both comply well with the expert's monotonicity knowledge and predict the training data accurately. The suggested approach leads to lower root-mean-squared errors than comparative methods from the literature for the sparse data sets considered in this work.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge