Modelling Non-Smooth Signals with Complex Spectral Structure

The Gaussian Process Convolution Model (GPCM; Tobar et al., 2015a) is a model for signals with complex spectral structure. A significant limitation of the GPCM is that it assumes a rapidly decaying spectrum: it can only model smooth signals. Moreover, inference in the GPCM currently requires (1) a mean-field assumption, resulting in poorly calibrated uncertainties, and (2) a tedious variational optimisation of large covariance matrices. We redesign the GPCM model to induce a richer distribution over the spectrum with relaxed assumptions about smoothness: the Causal Gaussian Process Convolution Model (CGPCM) introduces a causality assumption into the GPCM, and the Rough Gaussian Process Convolution Model (RGPCM) can be interpreted as a Bayesian nonparametric generalisation of the fractional Ornstein-Uhlenbeck process. We also propose a more effective variational inference scheme, going beyond the mean-field assumption: we design a Gibbs sampler which directly samples from the optimal variational solution, circumventing any variational optimisation entirely. The proposed variations of the GPCM are validated in experiments on synthetic and real-world data, showing promising results.

Data Optimisation for a Deep Learning Recommender System

This paper advocates privacy preserving requirements on collection of user data for recommender systems. The purpose of our study is twofold. First, we ask if restrictions on data collection will hurt test quality of RNN-based recommendations. We study how validation performance depends on the available amount of training data. We use a combination of top-K accuracy, catalog coverage and novelty for this purpose, since good recommendations for the user is not necessarily captured by a traditional accuracy metric. Second, we ask if we can improve the quality under minimal data by using secondary data sources. We propose knowledge transfer for this purpose and construct a representation to measure similarities between purchase behaviour in data. This to make qualified judgements of which source domain will contribute the most. Our results show that (i) there is a saturation in test performance when training size is increased above a critical point. We also discuss the interplay between different performance metrics, and properties of data. Moreover, we demonstrate that (ii) our representation is meaningful for measuring purchase behaviour. In particular, results show that we can leverage secondary data to improve validation performance if we select a relevant source domain according to our similarly measure.

A Machine Learning approach to Risk Minimisation in Electricity Markets with Coregionalized Sparse Gaussian Processes

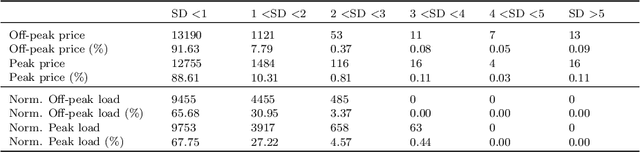
The non-storability of electricity makes it unique among commodity assets, and it is an important driver of its price behaviour in secondary financial markets. The instantaneous and continuous matching of power supply with demand is a key factor explaining its volatility. During periods of high demand, costlier generation capabilities are utilised since electricity cannot be stored and this has the impact of driving prices up very quickly. Furthermore, the non-storability also complicates physical hedging. Owing to these, the problem of joint price-quantity risk in electricity markets is a commonly studied theme. We propose using Gaussian Processes (GPs) to tackle this problem since GPs provide a versatile and elegant non-parametric approach for regression and time-series modelling. However, GPs scale poorly with the amount of training data due to a cubic complexity. These considerations suggest that knowledge transfer between price and load is vital for effective hedging, and that a computationally efficient method is required. To this end, we use the coregionalized (or multi-task) sparse GPs which addresses the aforementioned issues. To gauge the performance of our model, we use an average-load strategy as comparator. The latter is a robust approach commonly used by industry. If the spot and load are uncorrelated and Gaussian, then hedging with the expected load will result in the minimum variance position. Our main contributions are twofold. Firstly, in developing a coregionalized sparse GP-based approach for hedging. Secondly, in demonstrating that our model-based strategy outperforms the comparator, and can thus be employed for effective hedging in electricity markets.