A Machine Learning approach to Risk Minimisation in Electricity Markets with Coregionalized Sparse Gaussian Processes
Paper and Code
Apr 03, 2019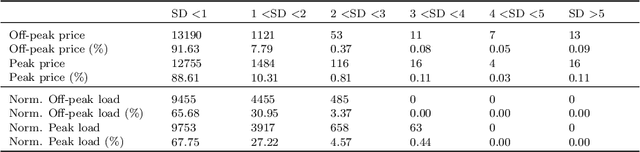
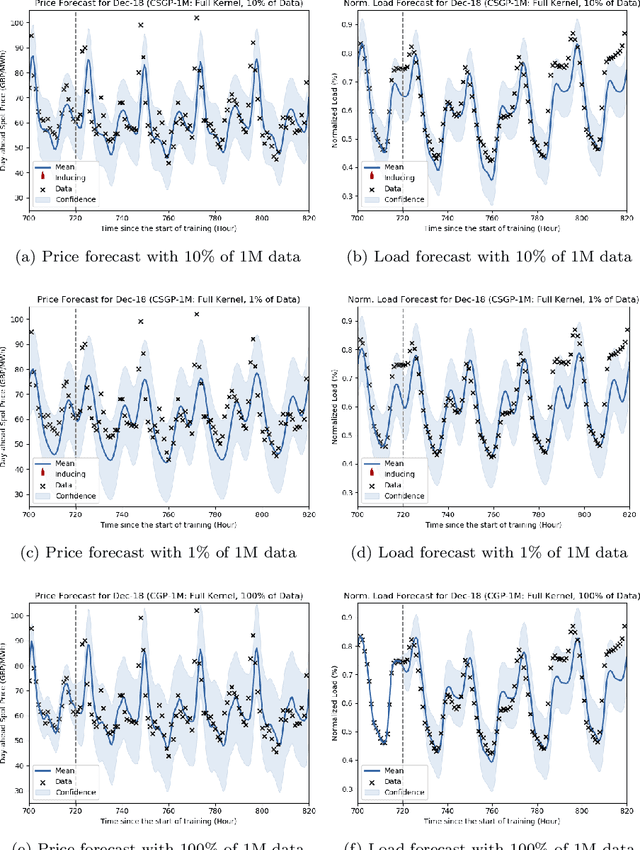
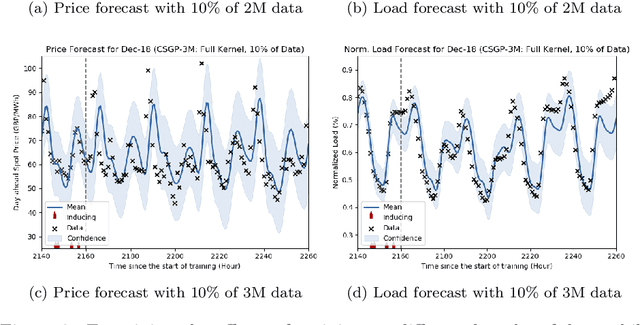
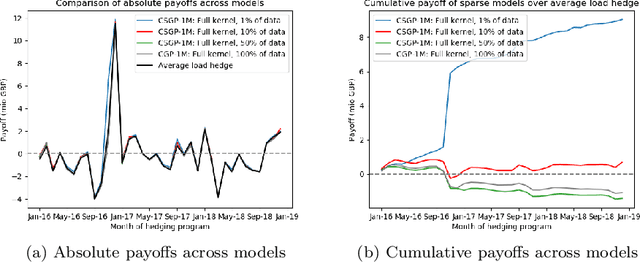
The non-storability of electricity makes it unique among commodity assets, and it is an important driver of its price behaviour in secondary financial markets. The instantaneous and continuous matching of power supply with demand is a key factor explaining its volatility. During periods of high demand, costlier generation capabilities are utilised since electricity cannot be stored and this has the impact of driving prices up very quickly. Furthermore, the non-storability also complicates physical hedging. Owing to these, the problem of joint price-quantity risk in electricity markets is a commonly studied theme. We propose using Gaussian Processes (GPs) to tackle this problem since GPs provide a versatile and elegant non-parametric approach for regression and time-series modelling. However, GPs scale poorly with the amount of training data due to a cubic complexity. These considerations suggest that knowledge transfer between price and load is vital for effective hedging, and that a computationally efficient method is required. To this end, we use the coregionalized (or multi-task) sparse GPs which addresses the aforementioned issues. To gauge the performance of our model, we use an average-load strategy as comparator. The latter is a robust approach commonly used by industry. If the spot and load are uncorrelated and Gaussian, then hedging with the expected load will result in the minimum variance position. Our main contributions are twofold. Firstly, in developing a coregionalized sparse GP-based approach for hedging. Secondly, in demonstrating that our model-based strategy outperforms the comparator, and can thus be employed for effective hedging in electricity markets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge