Martijn Bos
Efficient Geometric Linearization of Moving-Base Rigid Robot Dynamics
Apr 11, 2022
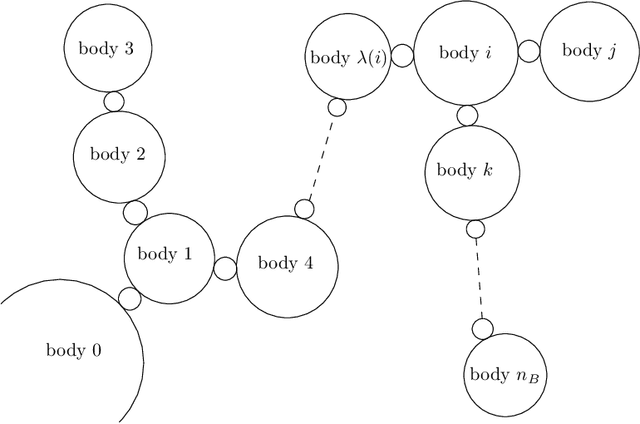
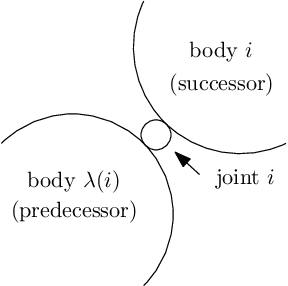
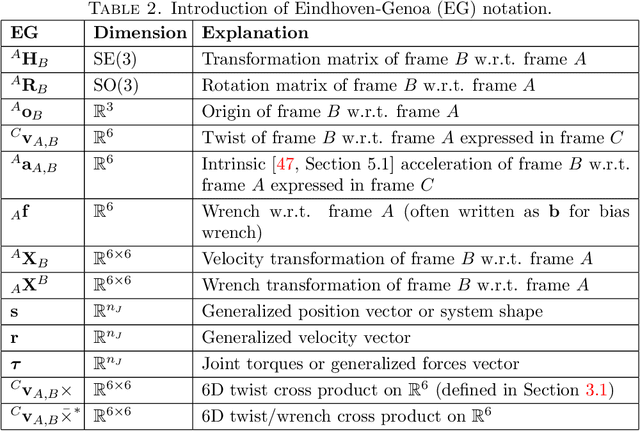
Abstract:The linearization of the equations of motion of a robotics system about a given state-input trajectory, including a controlled equilibrium state, is a valuable tool for model-based planning, closed-loop control, gain tuning, and state estimation. Contrary to the case of fixed based manipulators with prismatic or rotary joints, the state space of moving-base robotic systems such as humanoids, quadruped robots, or aerial manipulators cannot be globally parametrized by a finite number of independent coordinates. This impossibility is a direct consequence of the fact that the state of these systems includes the system's global orientation, formally described as an element of the special orthogonal group SO(3). As a consequence, obtaining the linearization of the equations of motion for these systems is typically resolved, from a practical perspective, by locally parameterizing the system's attitude by means of, e.g., Euler or Cardan angles. This has the drawback, however, of introducing artificial parameterization singularities and extra derivative computations. In this contribution, we show that it is actually possible to define a notion of linearization that does not require the use of a local parameterization for the system's orientation, obtaining a mathematically elegant, recursive, and singularity-free linearization for moving-based robot systems. Recursiveness, in particular, is obtained by proposing a nontrivial modification of existing recursive algorithms to allow for computations of the geometric derivatives of the inverse dynamics and the inverse of the mass matrix of the robotic system. The correctness of the proposed algorithm is validated by means of a numerical comparison with the result obtained via geometric finite difference.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge