Low-rank tensor recovery for Jacobian-based Volterra identification of parallel Wiener-Hammerstein systems

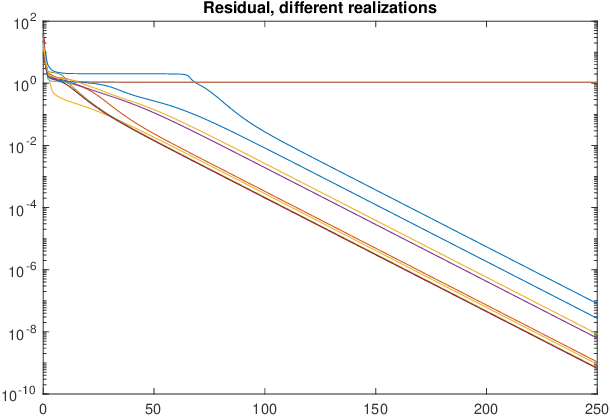
We consider the problem of identifying a parallel Wiener-Hammerstein structure from Volterra kernels. Methods based on Volterra kernels typically resort to coupled tensor decompositions of the kernels. However, in the case of parallel Wiener-Hammerstein systems, such methods require nontrivial constraints on the factors of the decompositions. In this paper, we propose an entirely different approach: by using special sampling (operating) points for the Jacobian of the nonlinear map from past inputs to the output, we can show that the Jacobian matrix becomes a linear projection of a tensor whose rank is equal to the number of branches. This representation allows us to solve the identification problem as a tensor recovery problem.

A Spectral Algorithm for Latent Junction Trees

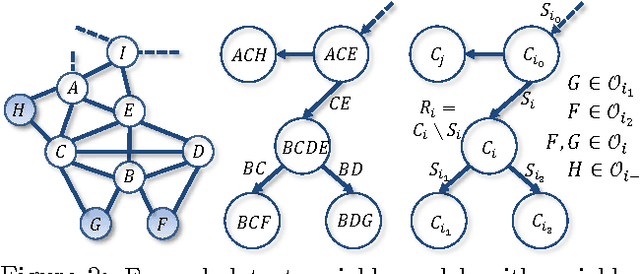
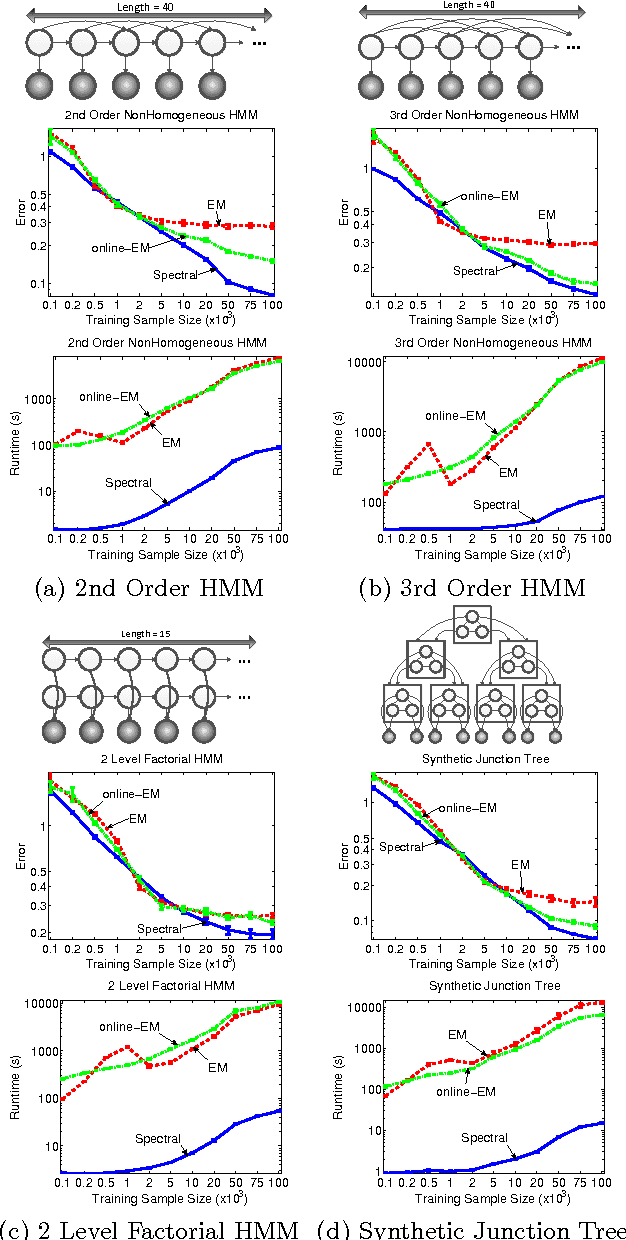
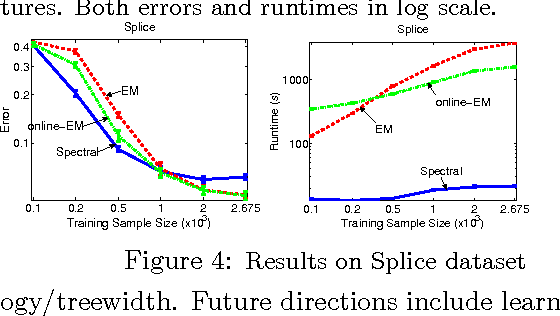
Latent variable models are an elegant framework for capturing rich probabilistic dependencies in many applications. However, current approaches typically parametrize these models using conditional probability tables, and learning relies predominantly on local search heuristics such as Expectation Maximization. Using tensor algebra, we propose an alternative parameterization of latent variable models (where the model structures are junction trees) that still allows for computation of marginals among observed variables. While this novel representation leads to a moderate increase in the number of parameters for junction trees of low treewidth, it lets us design a local-minimum-free algorithm for learning this parameterization. The main computation of the algorithm involves only tensor operations and SVDs which can be orders of magnitude faster than EM algorithms for large datasets. To our knowledge, this is the first provably consistent parameter learning technique for a large class of low-treewidth latent graphical models beyond trees. We demonstrate the advantages of our method on synthetic and real datasets.

Unfolding Latent Tree Structures using 4th Order Tensors

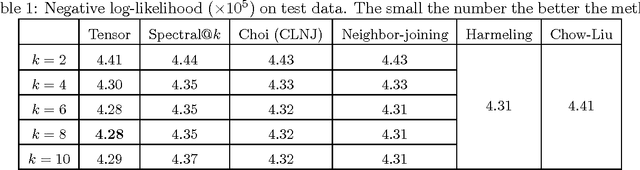
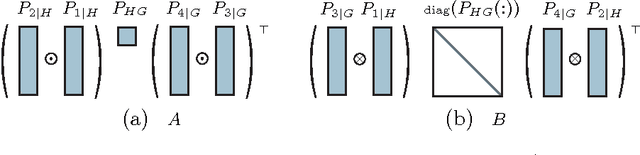
Discovering the latent structure from many observed variables is an important yet challenging learning task. Existing approaches for discovering latent structures often require the unknown number of hidden states as an input. In this paper, we propose a quartet based approach which is \emph{agnostic} to this number. The key contribution is a novel rank characterization of the tensor associated with the marginal distribution of a quartet. This characterization allows us to design a \emph{nuclear norm} based test for resolving quartet relations. We then use the quartet test as a subroutine in a divide-and-conquer algorithm for recovering the latent tree structure. Under mild conditions, the algorithm is consistent and its error probability decays exponentially with increasing sample size. We demonstrate that the proposed approach compares favorably to alternatives. In a real world stock dataset, it also discovers meaningful groupings of variables, and produces a model that fits the data better.