Unsupervised Unlearning of Concept Drift with Autoencoders

The phenomena of concept drift refers to a change of the data distribution affecting the data stream of future samples -- such non-stationary environments are often encountered in the real world. Consequently, learning models operating on the data stream might become obsolete, and need costly and difficult adjustments such as retraining or adaptation. Existing methods to address concept drift are, typically, categorised as active or passive. The former continually adapt a model using incremental learning, while the latter perform a complete model retraining when a drift detection mechanism triggers an alarm. We depart from the traditional avenues and propose for the first time an alternative approach which "unlearns" the effects of the concept drift. Specifically, we propose an autoencoder-based method for "unlearning" the concept drift in an unsupervised manner, without having to retrain or adapt any of the learning models operating on the data.

One Explanation to Rule them All -- Ensemble Consistent Explanations

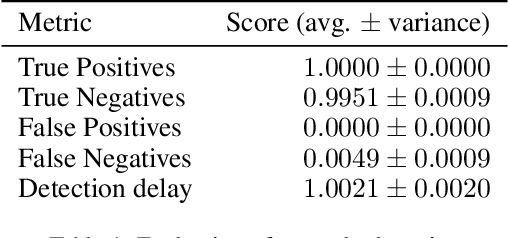
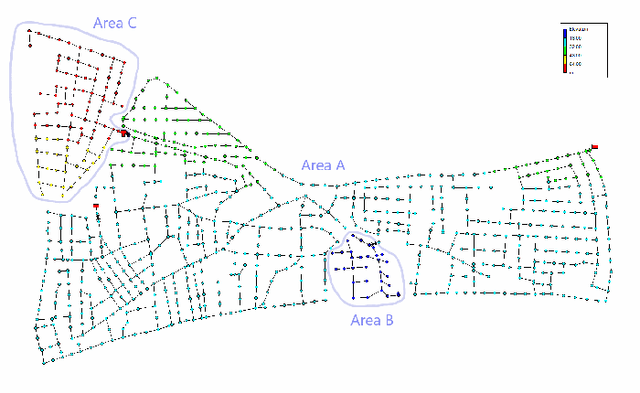
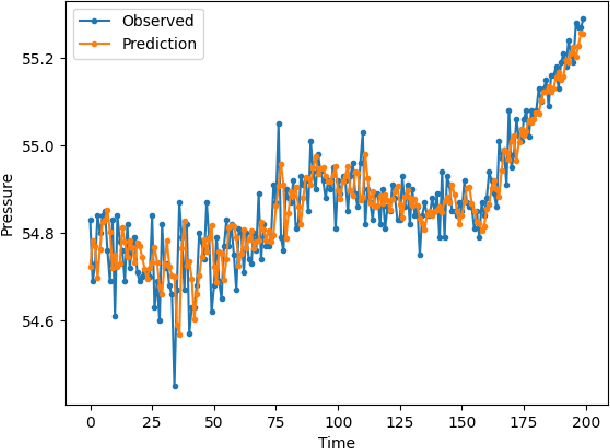
Transparency is a major requirement of modern AI based decision making systems deployed in real world. A popular approach for achieving transparency is by means of explanations. A wide variety of different explanations have been proposed for single decision making systems. In practice it is often the case to have a set (i.e. ensemble) of decisions that are used instead of a single decision only, in particular in complex systems. Unfortunately, explanation methods for single decision making systems are not easily applicable to ensembles -- i.e. they would yield an ensemble of individual explanations which are not necessarily consistent, hence less useful and more difficult to understand than a single consistent explanation of all observed phenomena. We propose a novel concept for consistently explaining an ensemble of decisions locally with a single explanation -- we introduce a formal concept, as well as a specific implementation using counterfactual explanations.

Nonlinear Discrete-time Systems' Identification without Persistence of Excitation: A Finite-time Concurrent Learning

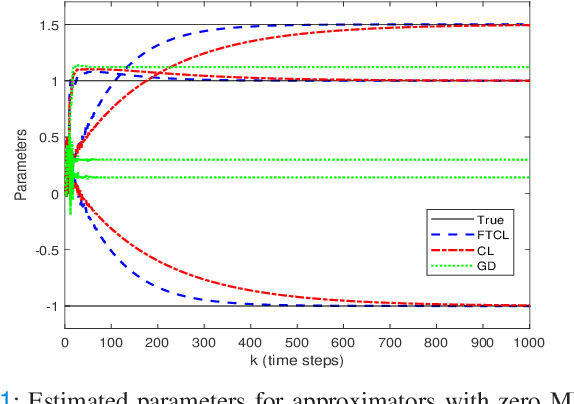
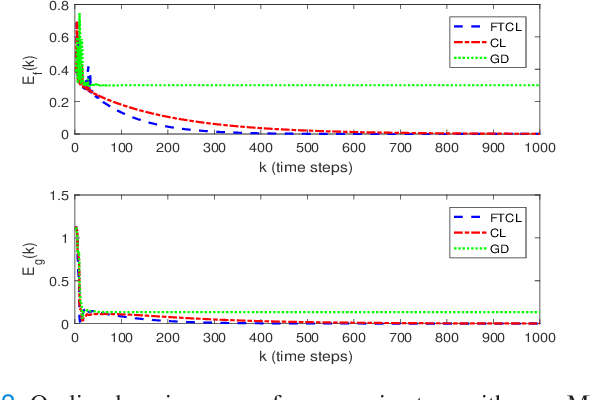
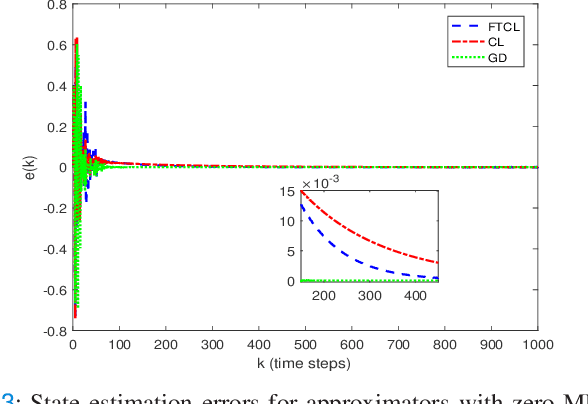
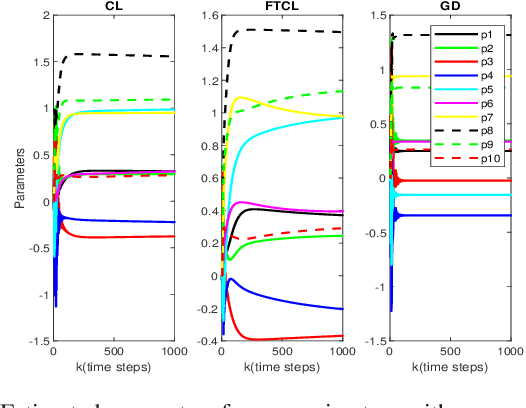
This paper deals with the problem of finite-time learning for unknown discrete-time nonlinear systems' dynamics, without the requirement of the persistence of excitation. A finite-time concurrent learning approach is presented to approximate the uncertainties of the discrete-time nonlinear systems in an on-line fashion by employing current data along with recorded experienced data satisfying an easy-to-check rank condition on the richness of the recorded data which is less restrictive in comparison with persistence of excitation condition. Rigorous proofs guarantee the finite-time convergence of the estimated parameters to their optimal values based on a discrete-time Lyapunov analysis. Compared with the existing work in the literature, simulation results illustrate that the proposed method can timely and precisely approximate the uncertainties.