FedDec: Peer-to-peer Aided Federated Learning

Federated learning (FL) has enabled training machine learning models exploiting the data of multiple agents without compromising privacy. However, FL is known to be vulnerable to data heterogeneity, partial device participation, and infrequent communication with the server, which are nonetheless three distinctive characteristics of this framework. While much of the recent literature has tackled these weaknesses using different tools, only a few works have explored the possibility of exploiting inter-agent communication to improve FL's performance. In this work, we present FedDec, an algorithm that interleaves peer-to-peer communication and parameter averaging (similar to decentralized learning in networks) between the local gradient updates of FL. We analyze the convergence of FedDec under the assumptions of non-iid data distribution, partial device participation, and smooth and strongly convex costs, and show that inter-agent communication alleviates the negative impact of infrequent communication rounds with the server by reducing the dependence on the number of local updates $H$ from $O(H^2)$ to $O(H)$. Furthermore, our analysis reveals that the term improved in the bound is multiplied by a constant that depends on the spectrum of the inter-agent communication graph, and that vanishes quickly the more connected the network is. We confirm the predictions of our theory in numerical simulations, where we show that FedDec converges faster than FedAvg, and that the gains are greater as either $H$ or the connectivity of the network increase.

Pick your Neighbor: Local Gauss-Southwell Rule for Fast Asynchronous Decentralized Optimization

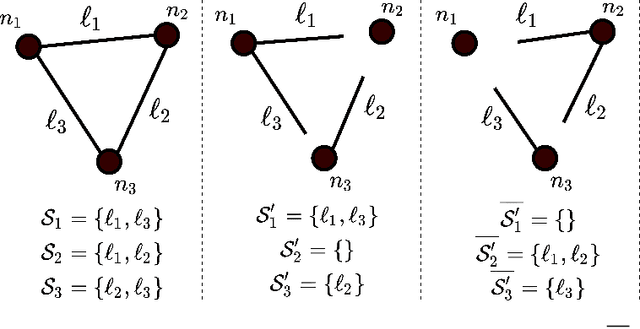
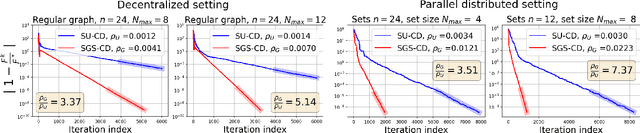
In decentralized optimization environments, each agent $i$ in a network of $n$ optimization nodes possesses a private function $f_i$, and nodes communicate with their neighbors to cooperatively minimize the aggregate objective $\sum_{i=1}^n f_i$. In this setting, synchronizing the nodes' updates incurs significant communication overhead and computational costs, so much of the recent literature has focused on the analysis and design of asynchronous optimization algorithms where agents activate and communicate at arbitrary times, without requiring a global synchronization enforcer. Nonetheless, in most of the work on the topic, active nodes select a neighbor to contact based on a fixed probability (e.g., uniformly at random), a choice that ignores the optimization landscape at the moment of activation. Instead, in this work we introduce an optimization-aware selection rule that chooses the neighbor with the highest dual cost improvement (a quantity related to a consensus-based dualization of the problem at hand). This scheme is related to the coordinate descent (CD) method with a Gauss-Southwell (GS) rule for coordinate updates; in our setting however, only a subset of coordinates is accessible at each iteration (because each node is constrained to communicate only with its direct neighbors), so the existing literature on GS methods does not apply. To overcome this difficulty, we develop a new analytical framework for smooth and strongly convex $f_i$ that covers the class of set-wise CD algorithms -- a class that directly applies to decentralized scenarios, but is not limited to them -- and we show that the proposed set-wise GS rule achieves a speedup by a factor of up to the maximum degree in the network (which is of the order of $\Theta(n)$ in highly connected graphs). The speedup predicted by our theoretical analysis is subsequently validated in numerical experiments with synthetic data.