Theoretical Lower Bounds for the Oven Scheduling Problem

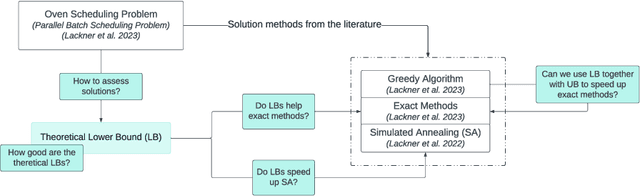
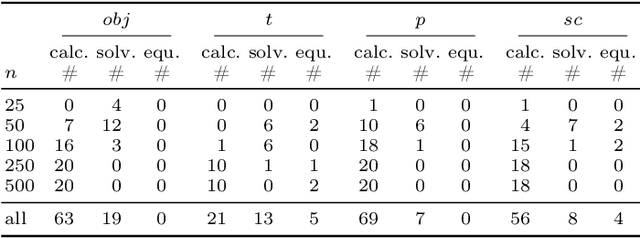
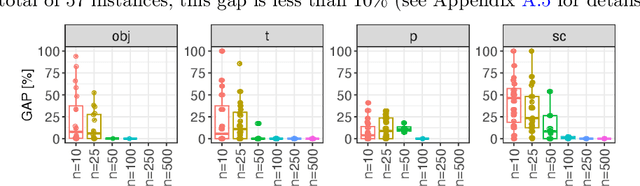
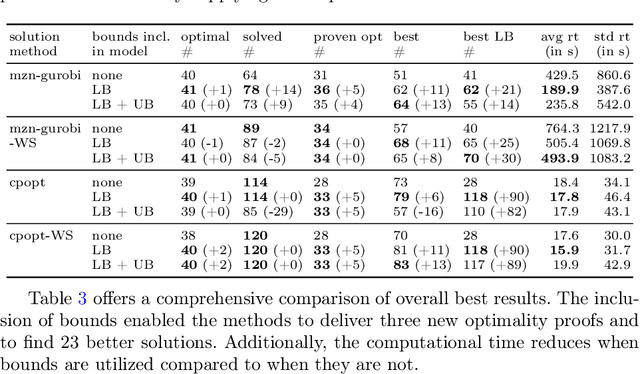
The Oven Scheduling Problem (OSP) is an NP-hard real-world parallel batch scheduling problem arising in the semiconductor industry. The objective of the problem is to schedule a set of jobs on ovens while minimizing several factors, namely total oven runtime, job tardiness, and setup costs. At the same time, it must adhere to various constraints such as oven eligibility and availability, job release dates, setup times between batches, and oven capacity limitations. The key to obtaining efficient schedules is to process compatible jobs simultaneously in batches. In this paper, we develop theoretical, problem-specific lower bounds for the OSP that can be computed very quickly. We thoroughly examine these lower bounds, evaluating their quality and exploring their integration into existing solution methods. Specifically, we investigate their contribution to exact methods and a metaheuristic local search approach using simulated annealing. Moreover, these problem-specific lower bounds enable us to assess the solution quality for large instances for which exact methods often fail to provide tight lower bounds.

Exact methods and lower bounds for the Oven Scheduling Problem

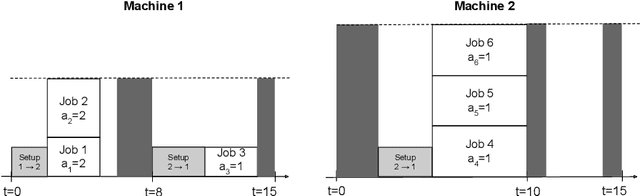
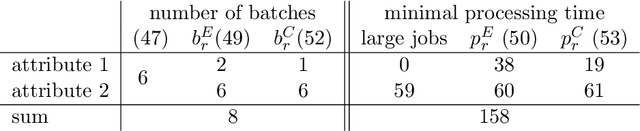
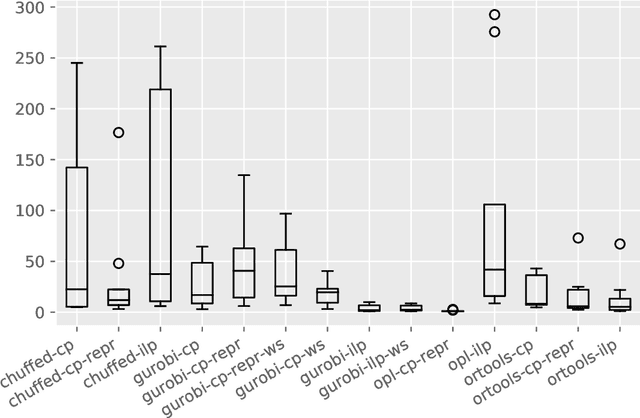
The Oven Scheduling Problem (OSP) is a new parallel batch scheduling problem that arises in the area of electronic component manufacturing. Jobs need to be scheduled to one of several ovens and may be processed simultaneously in one batch if they have compatible requirements. The scheduling of jobs must respect several constraints concerning eligibility and availability of ovens, release dates of jobs, setup times between batches as well as oven capacities. Running the ovens is highly energy-intensive and thus the main objective, besides finishing jobs on time, is to minimize the cumulative batch processing time across all ovens. This objective distinguishes the OSP from other batch processing problems which typically minimize objectives related to makespan, tardiness or lateness. We propose to solve this NP-hard scheduling problem via constraint programming (CP) and integer linear programming (ILP) and present corresponding models. For an experimental evaluation, we introduce a multi-parameter random instance generator to provide a diverse set of problem instances. Using state-of-the-art solvers, we evaluate the quality and compare the performance of our CP- and ILP-models. We show that our models can find feasible solutions for instances of realistic size, many of those being provably optimal or nearly optimal solutions. Finally, we derive theoretical lower bounds on the solution cost of feasible solutions to the OSP; these can be computed within a few seconds. We show that these lower bounds are competitive with those derived by state-of-the-art solvers.

Exact and Metaheuristic Approaches for the Production Leveling Problem

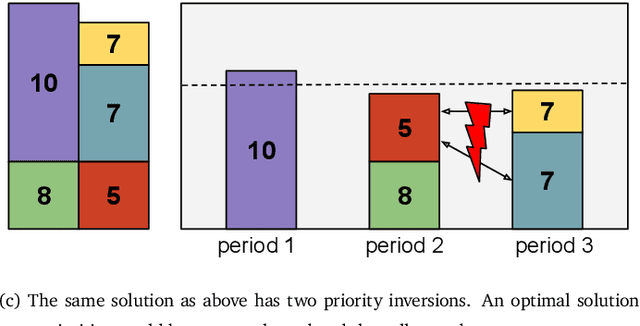
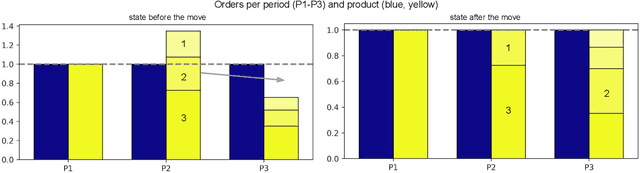
In this paper we introduce a new problem in the field of production planning which we call the Production Leveling Problem. The task is to assign orders to production periods such that the load in each period and on each production resource is balanced, capacity limits are not exceeded and the orders' priorities are taken into account. Production Leveling is an important intermediate step between long-term planning and the final scheduling of orders within a production period, as it is responsible for selecting good subsets of orders to be scheduled within each period. A formal model of the problem is proposed and NP-hardness is shown by reduction from Bin Backing. As an exact method for solving moderately sized instances we introduce a MIP formulation. For solving large problem instances, metaheuristic local search is investigated. A greedy heuristic and two neighborhood structures for local search are proposed, in order to apply them using Variable Neighborhood Descent and Simulated Annealing. Regarding exact techniques, the main question of research is, up to which size instances are solvable within a fixed amount of time. For the metaheuristic approaches the aim is to show that they produce near-optimal solutions for smaller instances, but also scale well to very large instances. A set of realistic problem instances from an industrial partner is contributed to the literature, as well as random instance generators. The experimental evaluation conveys that the proposed MIP model works well for instances with up to 250 orders. Out of the investigated metaheuristic approaches, Simulated Annealing achieves the best results. It is shown to produce solutions with less than 3% average optimality gap on small instances and to scale well up to thousands of orders and dozens of periods and products. The presented metaheuristic methods are already being used in the industry.