Assessing Reproducibility in Evolutionary Computation: A Case Study using Human- and LLM-based Assessment

Reproducibility is an important requirement in evolutionary computation, where results largely depend on computational experiments. In practice, reproducibility relies on how algorithms, experimental protocols, and artifacts are documented and shared. Despite growing awareness, there is still limited empirical evidence on the actual reproducibility levels of published work in the field. In this paper, we study the reproducibility practices in papers published in the Evolutionary Combinatorial Optimization and Metaheuristics track of the Genetic and Evolutionary Computation Conference over a ten-year period. We introduce a structured reproducibility checklist and apply it through a systematic manual assessment of the selected corpus. In addition, we propose RECAP (REproducibility Checklist Automation Pipeline), an LLM-based system that automatically evaluates reproducibility signals from paper text and associated code repositories. Our analysis shows that papers achieve an average completeness score of 0.62, and that 36.90% of them provide additional material beyond the manuscript itself. We demonstrate that automated assessment is feasible: RECAP achieves substantial agreement with human evaluators (Cohen's k of 0.67). Together, these results highlight persistent gaps in reproducibility reporting and suggest that automated tools can effectively support large-scale, systematic monitoring of reproducibility practices.

Behavior and Representation in Large Language Models for Combinatorial Optimization: From Feature Extraction to Algorithm Selection

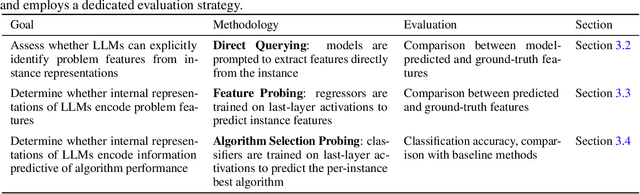
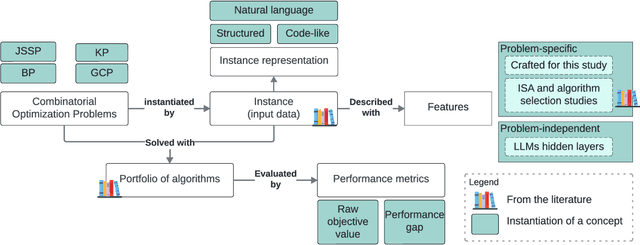
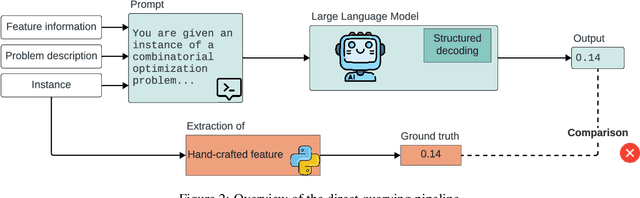
Recent advances in Large Language Models (LLMs) have opened new perspectives for automation in optimization. While several studies have explored how LLMs can generate or solve optimization models, far less is understood about what these models actually learn regarding problem structure or algorithmic behavior. This study investigates how LLMs internally represent combinatorial optimization problems and whether such representations can support downstream decision tasks. We adopt a twofold methodology combining direct querying, which assesses LLM capacity to explicitly extract instance features, with probing analyses that examine whether such information is implicitly encoded within their hidden layers. The probing framework is further extended to a per-instance algorithm selection task, evaluating whether LLM-derived representations can predict the best-performing solver. Experiments span four benchmark problems and three instance representations. Results show that LLMs exhibit moderate ability to recover feature information from problem instances, either through direct querying or probing. Notably, the predictive power of LLM hidden-layer representations proves comparable to that achieved through traditional feature extraction, suggesting that LLMs capture meaningful structural information relevant to optimization performance.

Theoretical Lower Bounds for the Oven Scheduling Problem

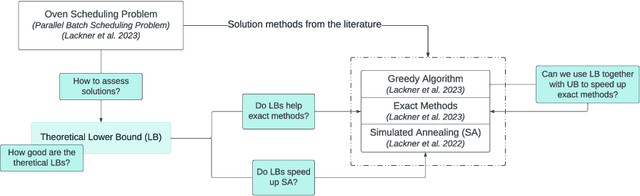
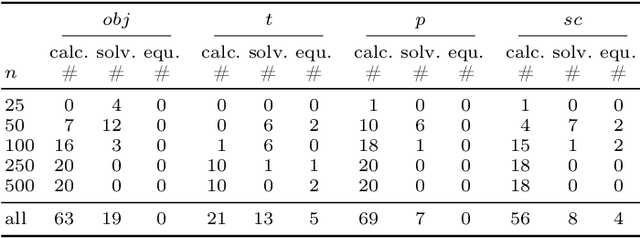
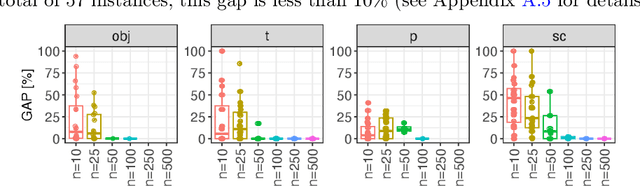
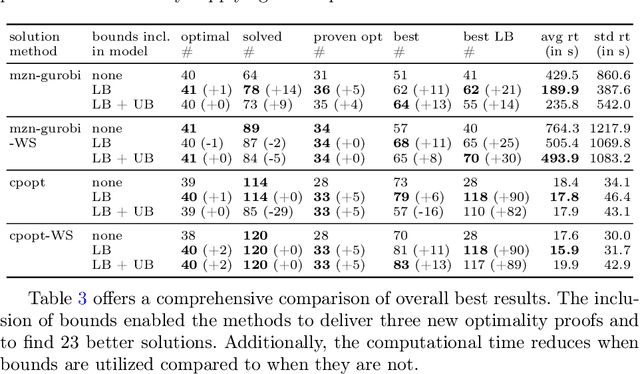
The Oven Scheduling Problem (OSP) is an NP-hard real-world parallel batch scheduling problem arising in the semiconductor industry. The objective of the problem is to schedule a set of jobs on ovens while minimizing several factors, namely total oven runtime, job tardiness, and setup costs. At the same time, it must adhere to various constraints such as oven eligibility and availability, job release dates, setup times between batches, and oven capacity limitations. The key to obtaining efficient schedules is to process compatible jobs simultaneously in batches. In this paper, we develop theoretical, problem-specific lower bounds for the OSP that can be computed very quickly. We thoroughly examine these lower bounds, evaluating their quality and exploring their integration into existing solution methods. Specifically, we investigate their contribution to exact methods and a metaheuristic local search approach using simulated annealing. Moreover, these problem-specific lower bounds enable us to assess the solution quality for large instances for which exact methods often fail to provide tight lower bounds.