Christoph Mrkvicka
Exact methods and lower bounds for the Oven Scheduling Problem
Mar 23, 2022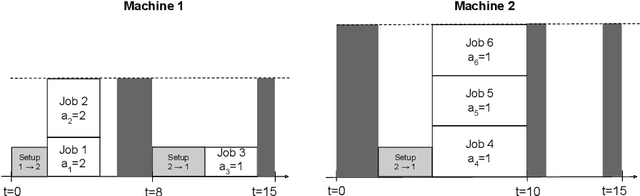
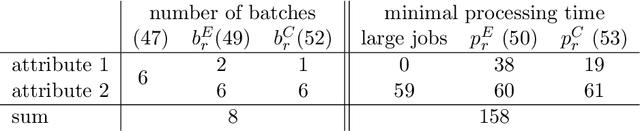
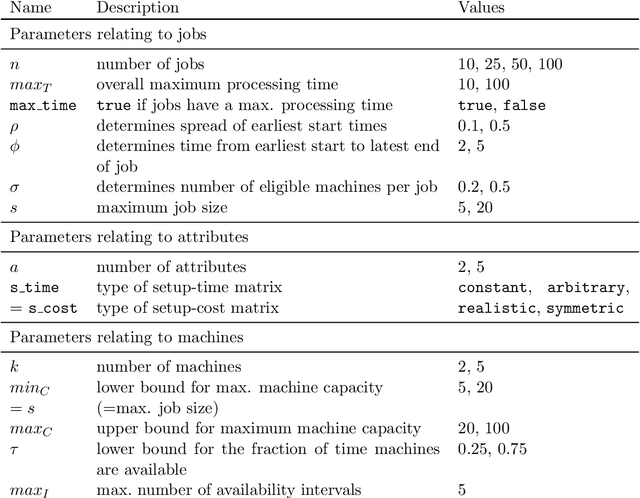
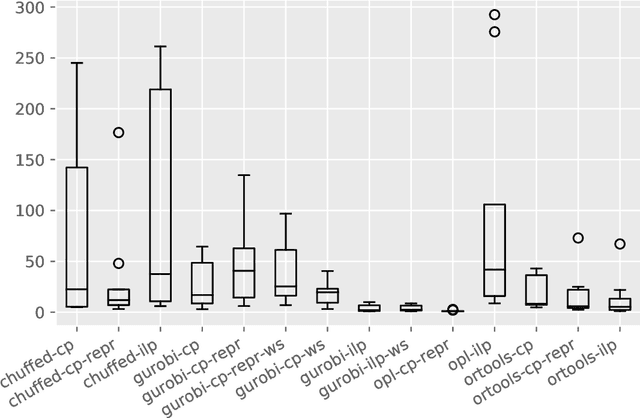
Abstract:The Oven Scheduling Problem (OSP) is a new parallel batch scheduling problem that arises in the area of electronic component manufacturing. Jobs need to be scheduled to one of several ovens and may be processed simultaneously in one batch if they have compatible requirements. The scheduling of jobs must respect several constraints concerning eligibility and availability of ovens, release dates of jobs, setup times between batches as well as oven capacities. Running the ovens is highly energy-intensive and thus the main objective, besides finishing jobs on time, is to minimize the cumulative batch processing time across all ovens. This objective distinguishes the OSP from other batch processing problems which typically minimize objectives related to makespan, tardiness or lateness. We propose to solve this NP-hard scheduling problem via constraint programming (CP) and integer linear programming (ILP) and present corresponding models. For an experimental evaluation, we introduce a multi-parameter random instance generator to provide a diverse set of problem instances. Using state-of-the-art solvers, we evaluate the quality and compare the performance of our CP- and ILP-models. We show that our models can find feasible solutions for instances of realistic size, many of those being provably optimal or nearly optimal solutions. Finally, we derive theoretical lower bounds on the solution cost of feasible solutions to the OSP; these can be computed within a few seconds. We show that these lower bounds are competitive with those derived by state-of-the-art solvers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge