A Lie Group-Based Race Car Model for Systematic Trajectory Optimization on 3D Tracks

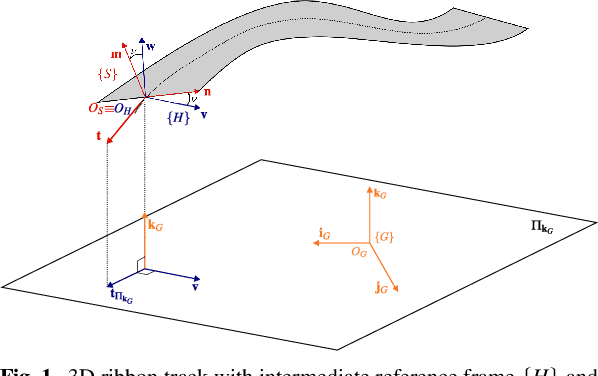
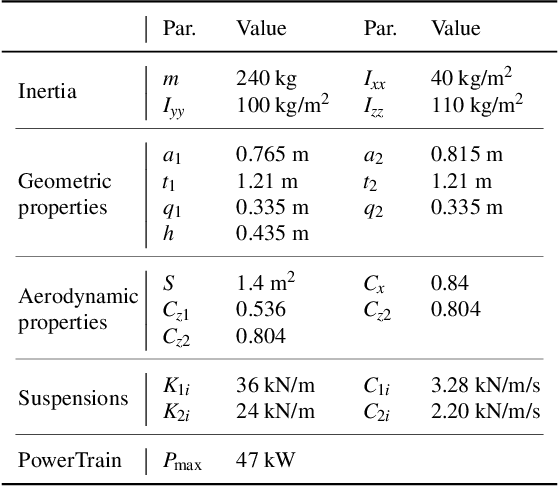
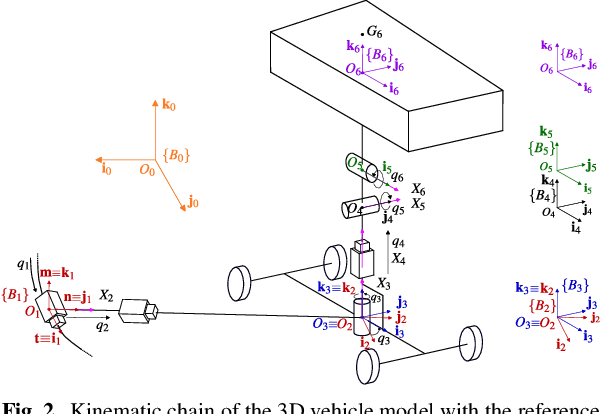
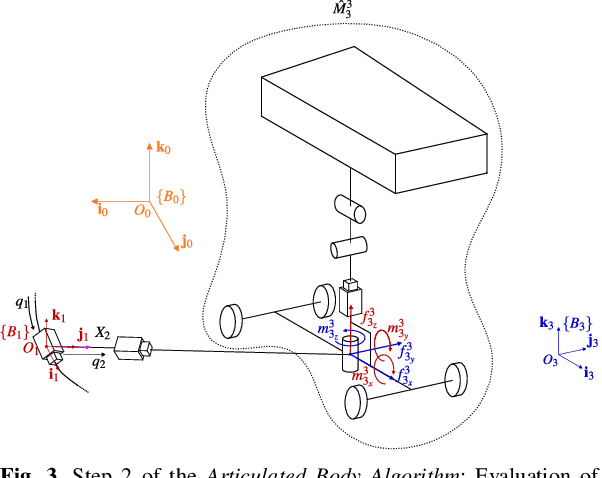
In this paper we derive the dynamic equations of a race-car model via Lie-group methods. Lie-group methods are nowadays quite familiar to computational dynamicists and roboticists, but their diffusion within the vehicle dynamics community is still limited. We try to bridge this gap by showing that this framework merges gracefully with the Articulated Body Algorithm (ABA) and enables a fresh and systematic formulation of the vehicle dynamics. A significant contribution is represented by a rigorous reconciliation of the ABA steps with the salient features of vehicle dynamics, such as road-tire interactions, aerodynamic forces and load transfers. The proposed approach lends itself both to the definition of direct simulation models and to the systematic assembly of vehicle dynamics equations required, in the form of equality constraints, in numerical optimal control problems. We put our approach on a test in the latter context which involves the solution of minimum lap-time problem (MLTP). More specifically, a MLTP for a race car on the N\"urburgring circuit is systematically set up with our approach. The equations are then discretized with the direct collocation method and solved within the CasADi optimization suite. Both the quality of the solution and the computational efficiency demonstrate the validity of the presented approach.

Learning and Inference of Dexterous Grasps for Novel Objects with Underactuated Hands

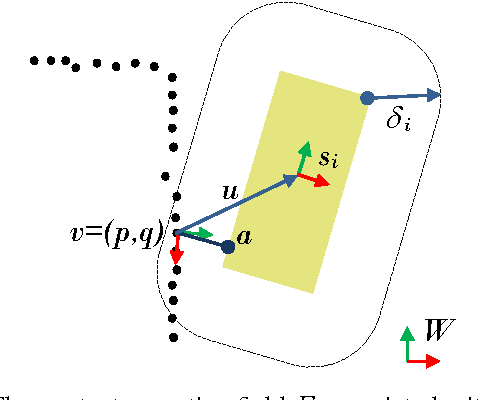
Recent advances have been made in learning of grasps for fully actuated hands. A typical approach learns the target locations of finger links on the object. When a new object must be grasped, new finger locations are generated, and a collision free reach-to-grasp trajectory is planned. This assumes a collision free trajectory to the final grasp. This is not possible with underactuated hands, which cannot be guaranteed to avoid contact, and in fact exploit contacts with the object during grasping, so as to reach an equilibrium state in which the object is held securely. Unfortunately, these contact interactions are i) not directly controllable, and ii) hard to monitor during a real grasp. We overcome these problems so as to permit learning of transferrable grasps for underactuated hands. We make two main technical innovations. First, we model contact interactions during the grasp implicitly. We do this by modelling motor commands that lead reliably to the equilibrium state, rather than modelling contact changes themselves. This alters our reach-to-grasp model. Second, we extend our contact model learning algorithm to work with multiple training examples for each grasp type. This requires the ability to learn which parts of the hand reliably interact with the object during a particular grasp. Our approach learns from a rigid body simulation. This enables us to learn how to approach the object and close the underactuated hand from a variety of poses. From nine training grasps on three objects the method transferred grasps to previously unseen, novel objects, that differ significantly from the training objects, with an 80% success rate.