Lorenzo Bartali
A Lie Group-Based Race Car Model for Systematic Trajectory Optimization on 3D Tracks
Feb 20, 2023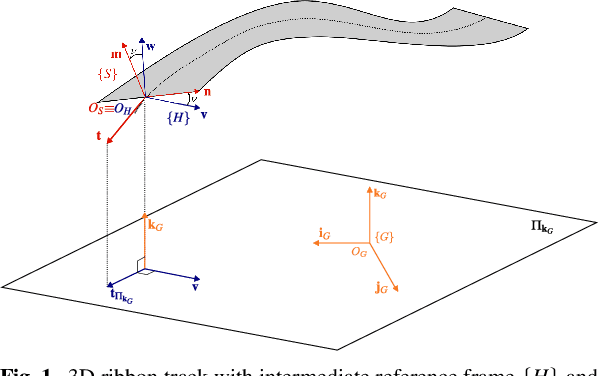
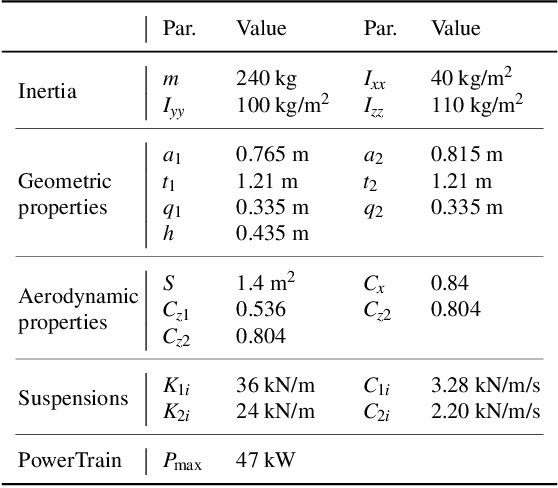
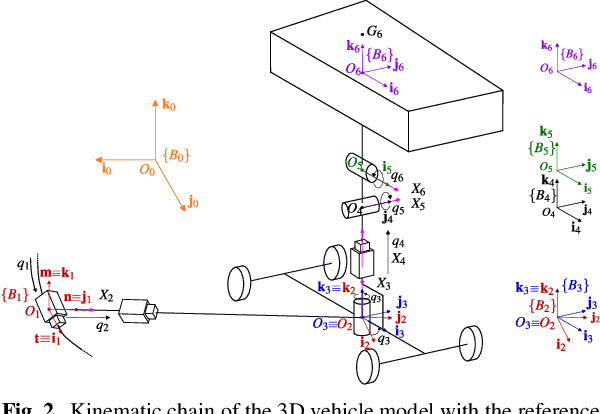
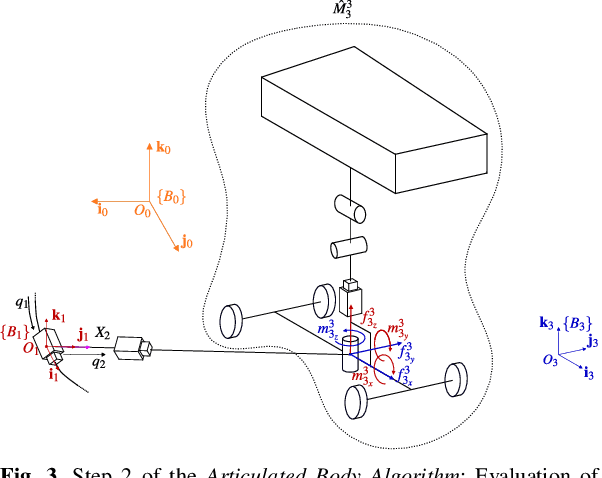
Abstract:In this paper we derive the dynamic equations of a race-car model via Lie-group methods. Lie-group methods are nowadays quite familiar to computational dynamicists and roboticists, but their diffusion within the vehicle dynamics community is still limited. We try to bridge this gap by showing that this framework merges gracefully with the Articulated Body Algorithm (ABA) and enables a fresh and systematic formulation of the vehicle dynamics. A significant contribution is represented by a rigorous reconciliation of the ABA steps with the salient features of vehicle dynamics, such as road-tire interactions, aerodynamic forces and load transfers. The proposed approach lends itself both to the definition of direct simulation models and to the systematic assembly of vehicle dynamics equations required, in the form of equality constraints, in numerical optimal control problems. We put our approach on a test in the latter context which involves the solution of minimum lap-time problem (MLTP). More specifically, a MLTP for a race car on the N\"urburgring circuit is systematically set up with our approach. The equations are then discretized with the direct collocation method and solved within the CasADi optimization suite. Both the quality of the solution and the computational efficiency demonstrate the validity of the presented approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge