A Unifying Framework for Structural Properties of CSPs: Definitions, Complexity, Tractability

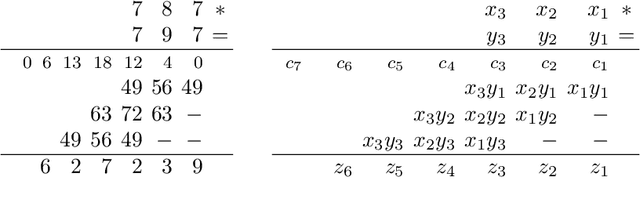
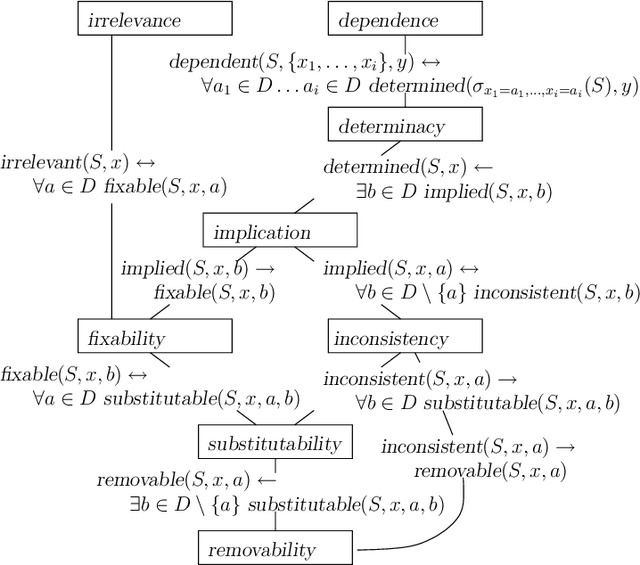
Literature on Constraint Satisfaction exhibits the definition of several structural properties that can be possessed by CSPs, like (in)consistency, substitutability or interchangeability. Current tools for constraint solving typically detect such properties efficiently by means of incomplete yet effective algorithms, and use them to reduce the search space and boost search. In this paper, we provide a unifying framework encompassing most of the properties known so far, both in CSP and other fields literature, and shed light on the semantical relationships among them. This gives a unified and comprehensive view of the topic, allows new, unknown, properties to emerge, and clarifies the computational complexity of the various detection problems. In particular, among the others, two new concepts, fixability and removability emerge, that come out to be the ideal characterisations of values that may be safely assigned or removed from a variables domain, while preserving problem satisfiability. These two notions subsume a large number of known properties, including inconsistency, substitutability and others. Because of the computational intractability of all the property-detection problems, by following the CSP approach we then determine a number of relaxations which provide sufficient conditions for their tractability. In particular, we exploit forms of language restrictions and local reasoning.

Generalizing Consistency and other Constraint Properties to Quantified Constraints

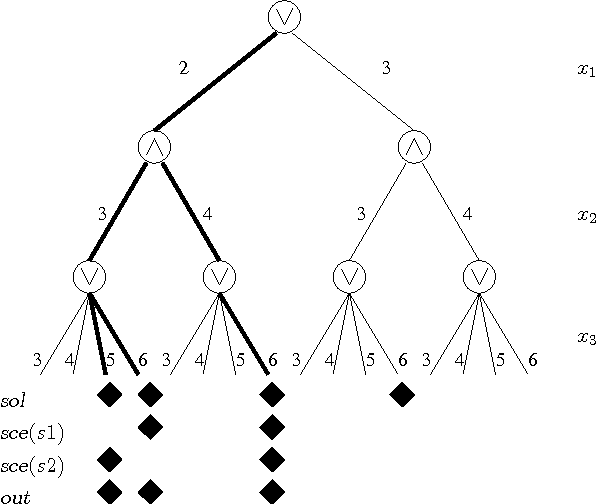
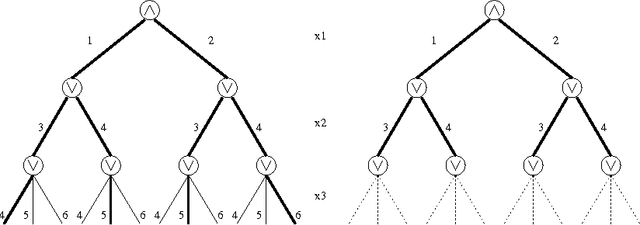
Quantified constraints and Quantified Boolean Formulae are typically much more difficult to reason with than classical constraints, because quantifier alternation makes the usual notion of solution inappropriate. As a consequence, basic properties of Constraint Satisfaction Problems (CSP), such as consistency or substitutability, are not completely understood in the quantified case. These properties are important because they are the basis of most of the reasoning methods used to solve classical (existentially quantified) constraints, and one would like to benefit from similar reasoning methods in the resolution of quantified constraints. In this paper, we show that most of the properties that are used by solvers for CSP can be generalized to quantified CSP. This requires a re-thinking of a number of basic concepts; in particular, we propose a notion of outcome that generalizes the classical notion of solution and on which all definitions are based. We propose a systematic study of the relations which hold between these properties, as well as complexity results regarding the decision of these properties. Finally, and since these problems are typically intractable, we generalize the approach used in CSP and propose weaker, easier to check notions based on locality, which allow to detect these properties incompletely but in polynomial time.

Combining Relational Algebra, SQL, Constraint Modelling, and Local Search

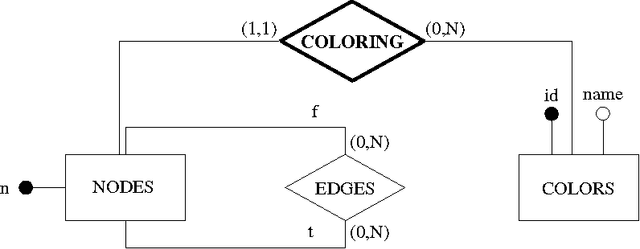
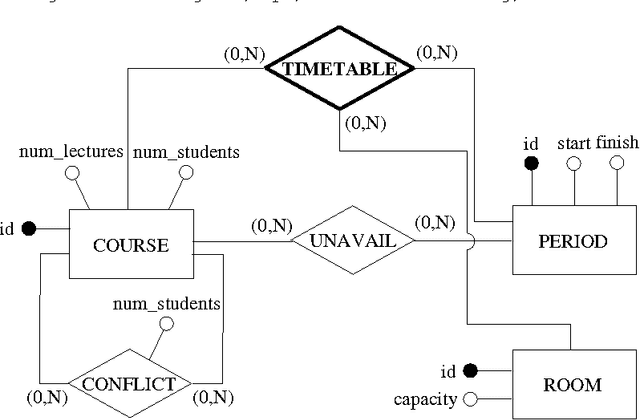
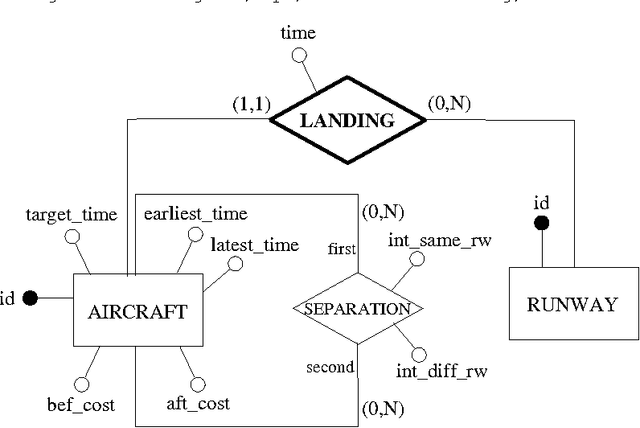
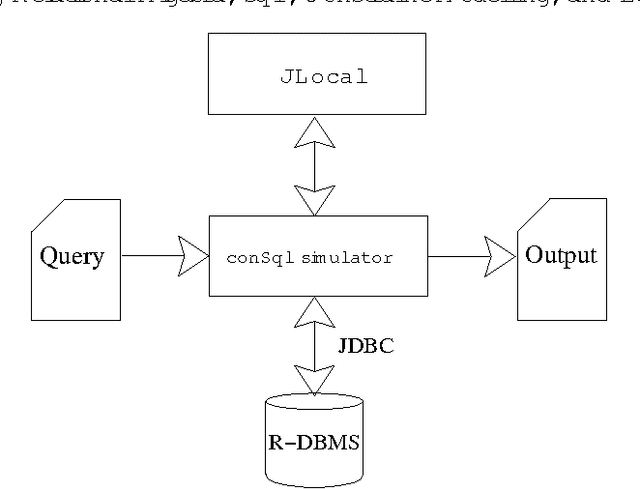
The goal of this paper is to provide a strong integration between constraint modelling and relational DBMSs. To this end we propose extensions of standard query languages such as relational algebra and SQL, by adding constraint modelling capabilities to them. In particular, we propose non-deterministic extensions of both languages, which are specially suited for combinatorial problems. Non-determinism is introduced by means of a guessing operator, which declares a set of relations to have an arbitrary extension. This new operator results in languages with higher expressive power, able to express all problems in the complexity class NP. Some syntactical restrictions which make data complexity polynomial are shown. The effectiveness of both extensions is demonstrated by means of several examples. The current implementation, written in Java using local search techniques, is described. To appear in Theory and Practice of Logic Programming (TPLP)

Complexity of Nested Circumscription and Nested Abnormality Theories

The need for a circumscriptive formalism that allows for simple yet elegant modular problem representation has led Lifschitz (AIJ, 1995) to introduce nested abnormality theories (NATs) as a tool for modular knowledge representation, tailored for applying circumscription to minimize exceptional circumstances. Abstracting from this particular objective, we propose L_{CIRC}, which is an extension of generic propositional circumscription by allowing propositional combinations and nesting of circumscriptive theories. As shown, NATs are naturally embedded into this language, and are in fact of equal expressive capability. We then analyze the complexity of L_{CIRC} and NATs, and in particular the effect of nesting. The latter is found to be a source of complexity, which climbs the Polynomial Hierarchy as the nesting depth increases and reaches PSPACE-completeness in the general case. We also identify meaningful syntactic fragments of NATs which have lower complexity. In particular, we show that the generalization of Horn circumscription in the NAT framework remains CONP-complete, and that Horn NATs without fixed letters can be efficiently transformed into an equivalent Horn CNF, which implies polynomial solvability of principal reasoning tasks. Finally, we also study extensions of NATs and briefly address the complexity in the first-order case. Our results give insight into the ``cost'' of using L_{CIRC} (resp. NATs) as a host language for expressing other formalisms such as action theories, narratives, or spatial theories.