Generalizing Consistency and other Constraint Properties to Quantified Constraints
Paper and Code
May 24, 2007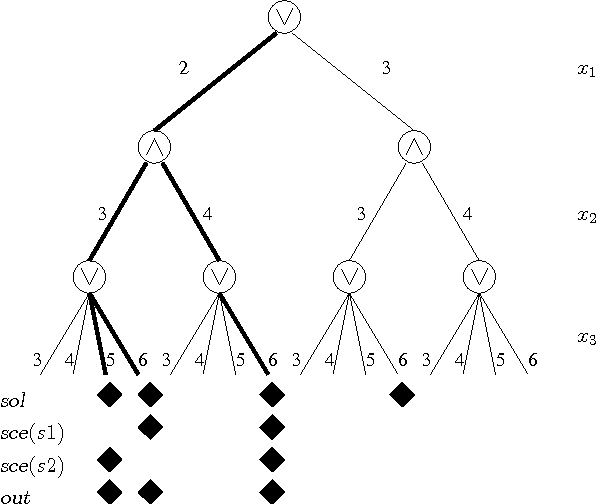
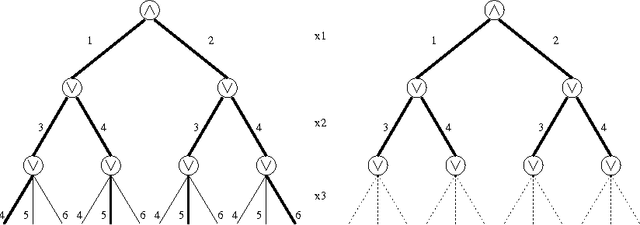
Quantified constraints and Quantified Boolean Formulae are typically much more difficult to reason with than classical constraints, because quantifier alternation makes the usual notion of solution inappropriate. As a consequence, basic properties of Constraint Satisfaction Problems (CSP), such as consistency or substitutability, are not completely understood in the quantified case. These properties are important because they are the basis of most of the reasoning methods used to solve classical (existentially quantified) constraints, and one would like to benefit from similar reasoning methods in the resolution of quantified constraints. In this paper, we show that most of the properties that are used by solvers for CSP can be generalized to quantified CSP. This requires a re-thinking of a number of basic concepts; in particular, we propose a notion of outcome that generalizes the classical notion of solution and on which all definitions are based. We propose a systematic study of the relations which hold between these properties, as well as complexity results regarding the decision of these properties. Finally, and since these problems are typically intractable, we generalize the approach used in CSP and propose weaker, easier to check notions based on locality, which allow to detect these properties incompletely but in polynomial time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge