A Unified Fractional Spectral Framework for Spatiotemporal Graph Signals: Bi-Fractional Transform and Geodesic Coupling

Graph signal processing extends spectral analysis to data supported on irregular domains. Existing fractional transforms for two-dimensional graph signals, including the two-dimensional graph fractional Fourier transform (GFRFT), typically impose a shared fractional order across dimensions, which limits adaptivity to heterogeneous spatiotemporal spectra. To address this limitation, we propose the two-dimensional graph bi-fractional Fourier transform, which assigns independent fractional orders to the factor graphs of a Cartesian product, enabling decoupled spectral control while preserving separability, unitarity, and invertibility. To further resolve the basis ambiguity in temporal fractional analysis, we develop a geodesic-coupled GFRFT by constructing a coupling path along the principal geodesic on the unitary manifold, thereby unifying graph-induced and discrete temporal bases with guaranteed unitarity and a closed-form inverse. Building on these transforms, we derive a differentiable Wiener-type filtering framework with a hybrid optimization strategy: the fractional orders are learned end-to-end from data, while the coupling parameter is fixed as a structural regularizer. Experiments on real-world time-varying graph datasets and dynamic image restoration tasks demonstrate consistent gains over state-of-the-art fractional transforms and competitive learning-based baselines.

FGFRFT: Fast Graph Fractional FourierTransform via Fourier Series Approximation

The graph fractional Fourier transform (GFRFT) generalizes the graph Fourier transform (GFT) but suffers from a significant computational bottleneck: determining the optimal transform order requires expensive eigendecomposition and matrix multiplication, leading to $O(N^3)$ complexity. To address this issue, we propose a fast GFRFT (FGFRFT) algorithm for unitary GFT matrices based on Fourier series approximation and an efficient caching strategy. FGFRFT reduces the complexity of generating transform matrices to $O(2LN^2)$ while preserving differentiability, thereby enabling adaptive order learning. We validate the algorithm through theoretical analysis, approximation accuracy tests, and order learning experiments. Furthermore, we demonstrate its practical efficacy for image and point cloud denoising and present the fractional specformer, which integrates the FGFRFT into the specformer architecture. This integration enables the model to overcome the limitations of a fixed GFT basis and learn optimal fractional orders for complex data. Experimental results confirm that the proposed algorithm significantly accelerates computation and achieves superior performance compared with the GFRFT.

Multiple-Parameter Graph Fractional Fourier Transform: Theory and Applications

The graph fractional Fourier transform (GFRFT) applies a single global fractional order to all graph frequencies, which restricts its adaptability to diverse signal characteristics across the spectral domain. To address this limitation, in this paper, we propose two types of multiple-parameter GFRFTs (MPGFRFTs) and establish their corresponding theoretical frameworks. We design a spectral compression strategy tailored for ultra-low compression ratios, effectively preserving essential information even under extreme dimensionality reduction. To enhance flexibility, we introduce a learnable order vector scheme that enables adaptive compression and denoising, demonstrating strong performance on both graph signals and images. We explore the application of MPGFRFTs to image encryption and decryption. Experimental results validate the versatility and superior performance of the proposed MPGFRFT framework across various graph signal processing tasks.

Graph Chirp Signal and Graph Fractional Vertex-Frequency Energy Distribution

Graph signal processing (GSP) has emerged as a powerful framework for analyzing data on irregular domains. In recent years, many classical techniques in signal processing (SP) have been successfully extended to GSP. Among them, chirp signals play a crucial role in various SP applications. However, graph chirp signals have not been formally defined despite their importance. Here, we define graph chirp signals and establish a comprehensive theoretical framework for their analysis. We propose the graph fractional vertex-frequency energy distribution (GFED), which provides a powerful tool for processing and analyzing graph chirp signals. We introduce the general fractional graph distribution (GFGD), a generalized vertex-frequency distribution, and the reduced interference GFED, which can suppress cross-term interference and enhance signal clarity. Furthermore, we propose a novel method for detecting graph signals through GFED domain filtering, facilitating robust detection and analysis of graph chirp signals in noisy environments. Moreover, this method can be applied to real-world data for denoising more effective than some state-of-the-arts, further demonstrating its practical significance.

Convolution Type of Metaplectic Cohen's Distribution Time-Frequency Analysis Theory, Method and Technology

The conventional Cohen's distribution can't meet the requirement of additive noises jamming signals high-performance denoising under the condition of low signal-to-noise ratio, it is necessary to integrate the metaplectic transform for non-stationary signal fractional domain time-frequency analysis. In this paper, we blend time-frequency operators and coordinate operator fractionizations to formulate the definition of the metaplectic Wigner distribution, based on which we integrate the generalized metaplectic convolution to address the unified representation issue of the convolution type of metaplectic Cohen's distribution (CMCD), whose special cases and essential properties are also derived. We blend Wiener filter principle and fractional domain filter mechanism of the metaplectic transform to design the least-squares adaptive filter method in the metaplectic Wigner distribution domain, giving birth to the least-squares adaptive filter-based CMCD whose kernel function can be adjusted with the input signal automatically to achieve the minimum mean-square error (MSE) denoising in Wigner distribution domain. We discuss the optimal symplectic matrices selection strategy of the proposed adaptive CMCD through the minimum MSE minimization modeling and solving. Some examples are also carried out to demonstrate that the proposed filtering method outperforms some state-of-the-arts including Wiener filter and fixed kernel functions-based or adaptive Cohen's distribution in noise suppression.

Adaptive Cohen's Class Time-Frequency Distribution

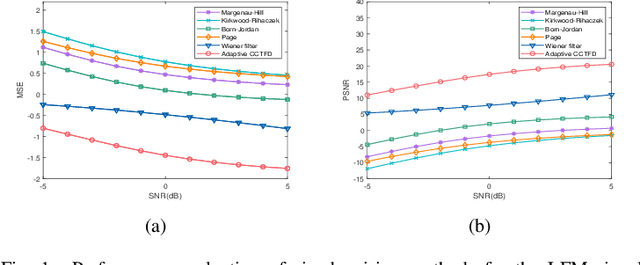
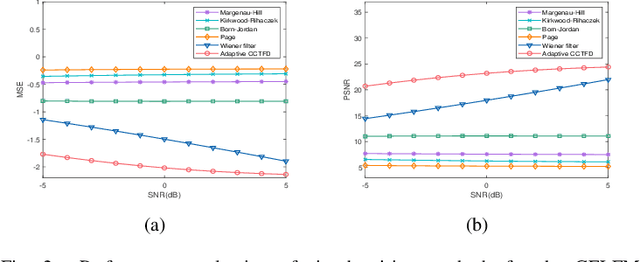
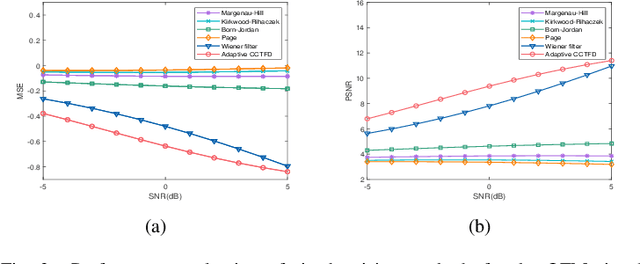
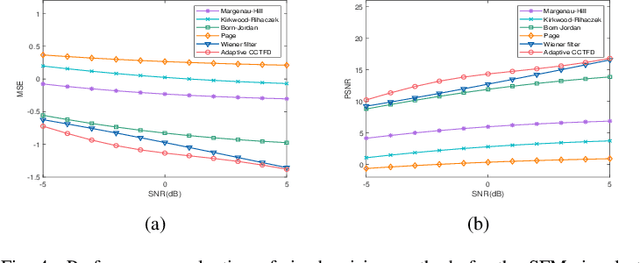
The fixed kernel function-based Cohen's class time-frequency distributions (CCTFDs) allow flexibility in denoising for some specific polluted signals. Due to the limitation of fixed kernel functions, however, from the view point of filtering they fail to automatically adjust the response according to the change of signal to adapt to different signal characteristics. In this letter, we integrate Wiener filter principle and the time-frequency filtering mechanism of CCTFD to design the least-squares adaptive filter method in the Wigner-Ville distribution (WVD) domain, giving birth to the least-squares adaptive filter-based CCTFD whose kernel function can be adjusted with the input signal automatically to achieve the minimum mean-square error denoising in the WVD domain. Some examples are also carried out to demonstrate that the proposed adaptive CCTFD outperforms some state-of-the-arts in noise suppression.