Manjesh Hanawal
Radar Enhanced Multi-Armed Bandit for Rapid Beam Selection in Millimeter Wave Communications
Jun 29, 2023Abstract:Multi-arm bandit (MAB) algorithms have been used to learn optimal beams for millimeter wave communication systems. Here, the complexity of learning the optimal beam linearly scales with the number of beams, leading to high latency when there are a large number of beams. In this work, we propose to integrate radar with communication to enhance the MAB learning performance by searching only those beams where the radar detects a scatterer. Further, we use radar to distinguish the beams that show mobile targets from those which indicate the presence of static clutter, thereby reducing the number of beams to scan. Simulations show that our proposed radar-enhanced MAB reduces the exploration time by searching only the beams with distinct radar mobile targets resulting in improved throughput.
Sequential Learning without Feedback
Oct 18, 2016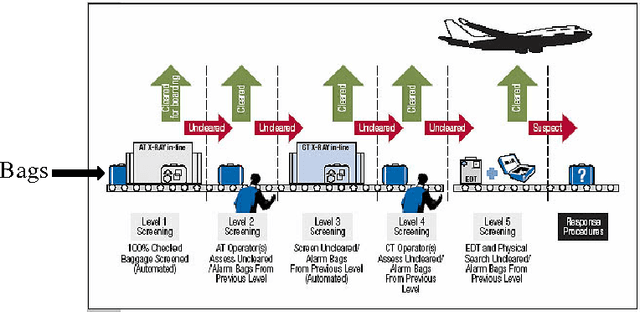
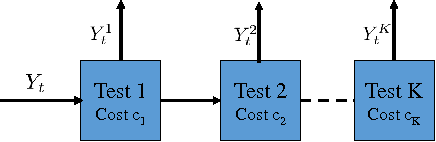
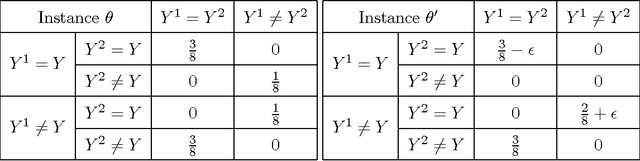

Abstract:In many security and healthcare systems a sequence of features/sensors/tests are used for detection and diagnosis. Each test outputs a prediction of the latent state, and carries with it inherent costs. Our objective is to {\it learn} strategies for selecting tests to optimize accuracy \& costs. Unfortunately it is often impossible to acquire in-situ ground truth annotations and we are left with the problem of unsupervised sensor selection (USS). We pose USS as a version of stochastic partial monitoring problem with an {\it unusual} reward structure (even noisy annotations are unavailable). Unsurprisingly no learner can achieve sublinear regret without further assumptions. To this end we propose the notion of weak-dominance. This is a condition on the joint probability distribution of test outputs and latent state and says that whenever a test is accurate on an example, a later test in the sequence is likely to be accurate as well. We empirically verify that weak dominance holds on real datasets and prove that it is a maximal condition for achieving sublinear regret. We reduce USS to a special case of multi-armed bandit problem with side information and develop polynomial time algorithms that achieve sublinear regret.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge