Sequential Learning without Feedback
Paper and Code
Oct 18, 2016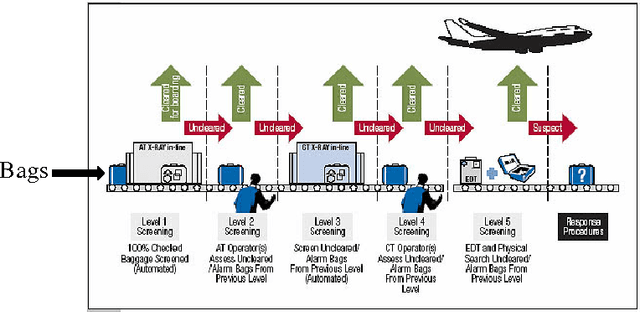
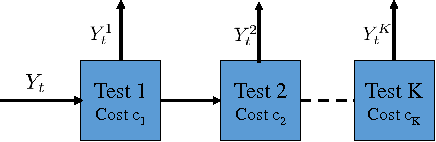
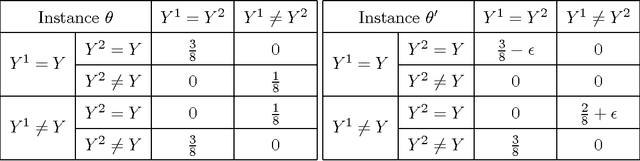

In many security and healthcare systems a sequence of features/sensors/tests are used for detection and diagnosis. Each test outputs a prediction of the latent state, and carries with it inherent costs. Our objective is to {\it learn} strategies for selecting tests to optimize accuracy \& costs. Unfortunately it is often impossible to acquire in-situ ground truth annotations and we are left with the problem of unsupervised sensor selection (USS). We pose USS as a version of stochastic partial monitoring problem with an {\it unusual} reward structure (even noisy annotations are unavailable). Unsurprisingly no learner can achieve sublinear regret without further assumptions. To this end we propose the notion of weak-dominance. This is a condition on the joint probability distribution of test outputs and latent state and says that whenever a test is accurate on an example, a later test in the sequence is likely to be accurate as well. We empirically verify that weak dominance holds on real datasets and prove that it is a maximal condition for achieving sublinear regret. We reduce USS to a special case of multi-armed bandit problem with side information and develop polynomial time algorithms that achieve sublinear regret.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge