Algebraic, Topological, and Mereological Foundations of Existential Granules

In this research, new concepts of existential granules that determine themselves are invented, and are characterized from algebraic, topological, and mereological perspectives. Existential granules are those that determine themselves initially, and interact with their environment subsequently. Examples of the concept, such as those of granular balls, though inadequately defined, algorithmically established, and insufficiently theorized in earlier works by others, are already used in applications of rough sets and soft computing. It is shown that they fit into multiple theoretical frameworks (axiomatic, adaptive, and others) of granular computing. The characterization is intended for algorithm development, application to classification problems and possible mathematical foundations of generalizations of the approach. Additionally, many open problems are posed and directions provided.

Algebraic Models for Qualified Aggregation in General Rough Sets, and Reasoning Bias Discovery

In the context of general rough sets, the act of combining two things to form another is not straightforward. The situation is similar for other theories that concern uncertainty and vagueness. Such acts can be endowed with additional meaning that go beyond structural conjunction and disjunction as in the theory of $*$-norms and associated implications over $L$-fuzzy sets. In the present research, algebraic models of acts of combining things in generalized rough sets over lattices with approximation operators (called rough convenience lattices) is invented. The investigation is strongly motivated by the desire to model skeptical or pessimistic, and optimistic or possibilistic aggregation in human reasoning, and the choice of operations is constrained by the perspective. Fundamental results on the weak negations and implications afforded by the minimal models are proved. In addition, the model is suitable for the study of discriminatory/toxic behavior in human reasoning, and of ML algorithms learning such behavior.

Rough Randomness and its Application

A number of generalizations of stochastic and information-theoretic randomness are known in the literature. However, they are not compatible with handling meaning in vague and dynamic contexts of rough reasoning (and therefore explainable artificial intelligence and machine learning). In this research, new concepts of rough randomness that are neither stochastic nor based on properties of strings are introduced by the present author. Her concepts are intended to capture a wide variety of rough processes (applicable to both static and dynamic data), construct related models, and explore the validity of other machine learning algorithms. The last mentioned is restricted to soft/hard clustering algorithms in this paper. Two new computationally efficient algebraically-justified algorithms for soft and hard cluster validation that involve rough random functions are additionally proposed in this research. A class of rough random functions termed large-minded reasoners have a central role in these.

Granular Directed Rough Sets, Concept Organization and Soft Clustering

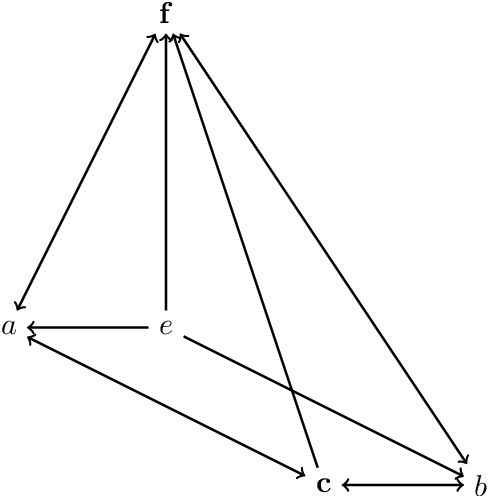
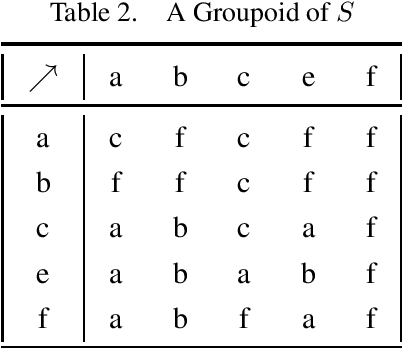
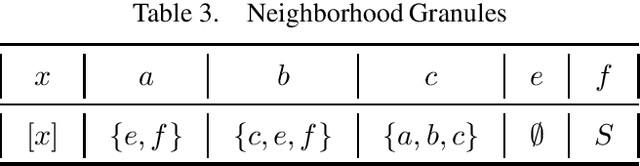
Up-directed rough sets are introduced and studied by the present author in earlier papers. This is extended by her in two different granular directions in this research, with a surprising algebraic semantics. The granules are based on ideas of generalized closure under up-directedness that may be read as a form of weak consequence. This yields approximation operators that satisfy cautious monotony, while pi-groupoidal approximations (that additionally involve strategic choice and algebraic operators) have nicer properties. The study is primarily motivated by possible structure of concepts in distributed cognition perspectives, real or virtual classroom learning contexts, and student-centric teaching. Rough clustering techniques for datasets that involve up-directed relations (as in the study of Sentinel project image data) are additionally proposed. This research is expected to see significant theoretical and practical applications in related domains.

Granular Generalized Variable Precision Rough Sets and Rational Approximations

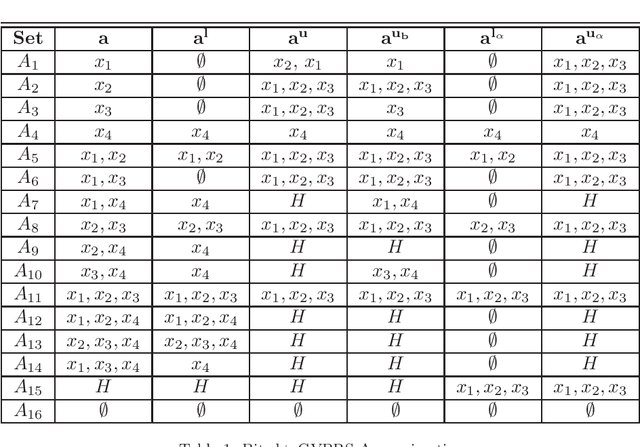
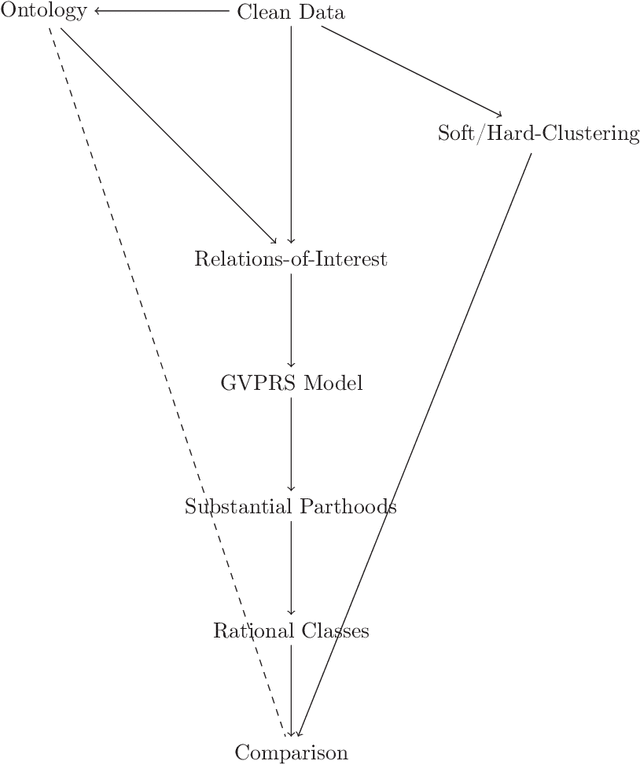
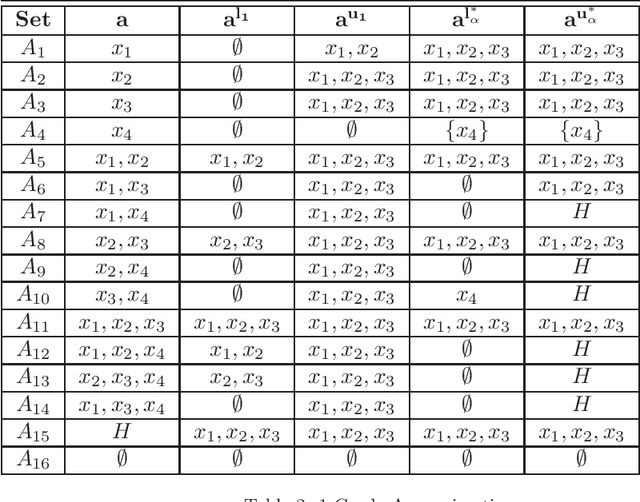
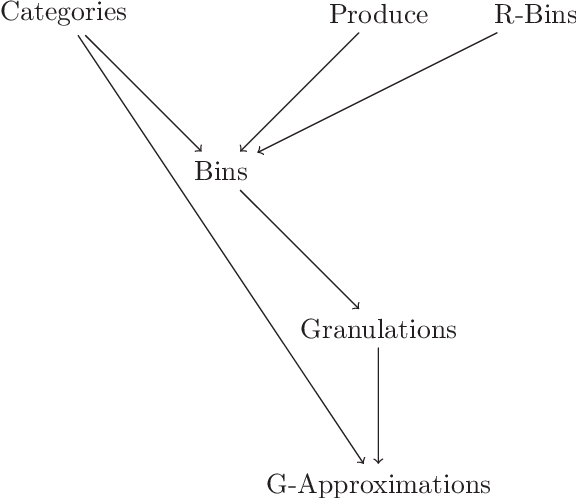
Rational approximations are introduced and studied in granular graded sets and generalizations thereof by the first author in recent research papers. The concept of rationality is determined by related ontologies and coherence between granularity, parthood perspective and approximations used in the context. In addition, a framework is introduced by her in the mentioned paper(s). Granular approximations constructed as per the procedures of VPRS are likely to be more rational than those constructed from a classical perspective under certain conditions. This may continue to hold for some generalizations of the former; however, a formal characterization of such conditions is not available in the previously published literature. In this research, theoretical aspects of the problem are critically examined, uniform generalizations of granular VPRS are introduced, new connections with granular graded rough sets are proved, appropriate concepts of substantial parthood are introduced, and their extent of compatibility with the framework is accessed. Furthermore, meta applications to cluster validation, image segmentation and dynamic sorting are invented. Basic assumptions made are explained, and additional examples are constructed for readability.

Algebraic Approach to Directed Rough Sets

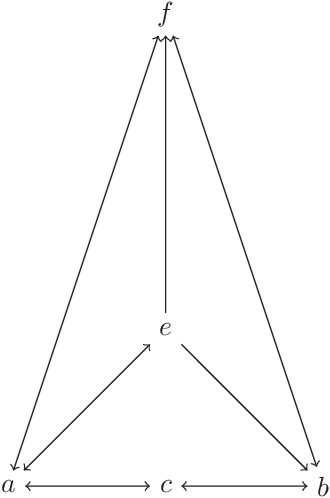
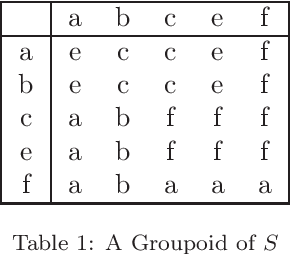
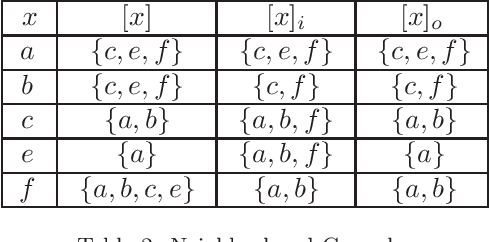
In relational approach to general rough sets, ideas of directed relations are supplemented with additional conditions for multiple algebraic approaches in this research paper. The relations are also specialized to representations of general parthood that are upper-directed, reflexive and antisymmetric for a better behaved groupoidal semantics over the set of roughly equivalent objects by the first author. Another distinct algebraic semantics over the set of approximations, and a new knowledge interpretation are also invented in this research by her. Because of minimal conditions imposed on the relations, neighborhood granulations are used in the construction of all approximations (granular and pointwise). Necessary and sufficient conditions for the lattice of local upper approximations to be completely distributive are proved by the second author. These results are related to formal concept analysis. Applications to student centered learning and decision making are also outlined.

Granularity and Generalized Inclusion Functions - Their Variants and Contamination

Rough inclusion functions (RIFs) are known by many other names in formal approaches to vagueness, belief, and uncertainty. Their use is often poorly grounded in factual knowledge or involve wild statistical assumptions. The concept of contamination introduced and studied by the present author across a number of her papers, concerns mixing up of information across semantic domains (or domains of discourse). RIFs play a key role in contaminating algorithms and some solutions that seek to replace or avoid them have been proposed and investigated by the present author in some of her earlier papers. The proposals break many algorithms of rough sets in a serious way. In this research, algorithm-friendly granular generalizations of such functions that reduce contamination are proposed and investigated from a mathematically sound perspective. Interesting representation results are proved and a core algebraic strategy for generalizing Skowron-Polkowski style of rough mereology is formulated.

A Study of FOSS'2013 Survey Data Using Clustering Techniques

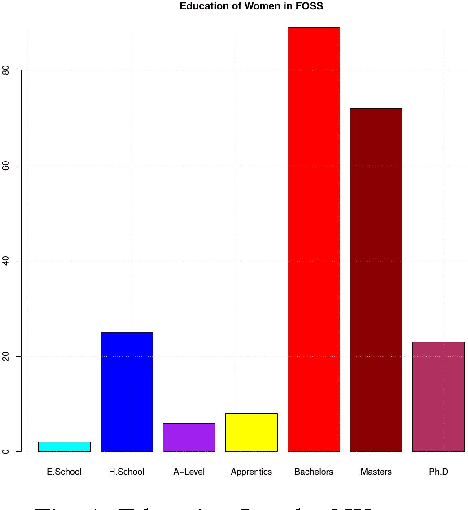
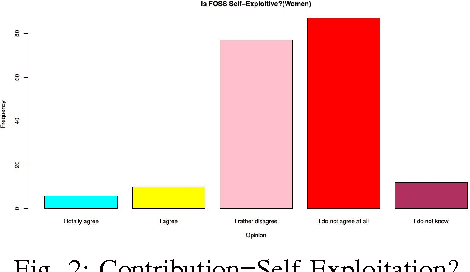
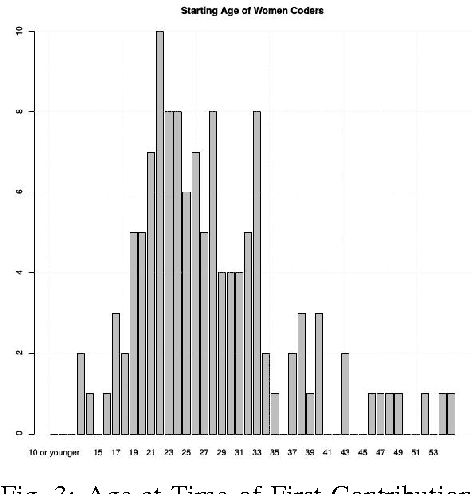
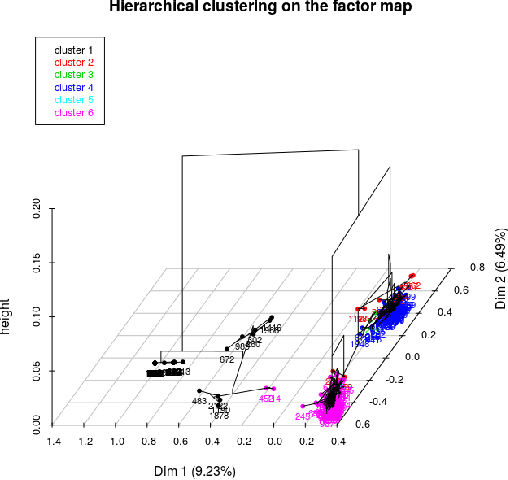
FOSS is an acronym for Free and Open Source Software. The FOSS 2013 survey primarily targets FOSS contributors and relevant anonymized dataset is publicly available under CC by SA license. In this study, the dataset is analyzed from a critical perspective using statistical and clustering techniques (especially multiple correspondence analysis) with a strong focus on women contributors towards discovering hidden trends and facts. Important inferences are drawn about development practices and other facets of the free software and OSS worlds.