Granular Generalized Variable Precision Rough Sets and Rational Approximations

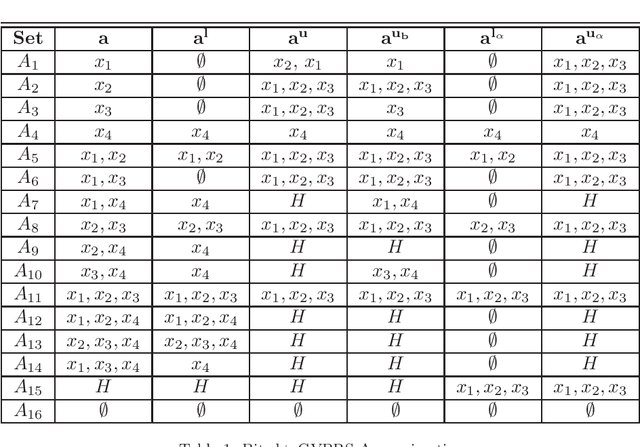
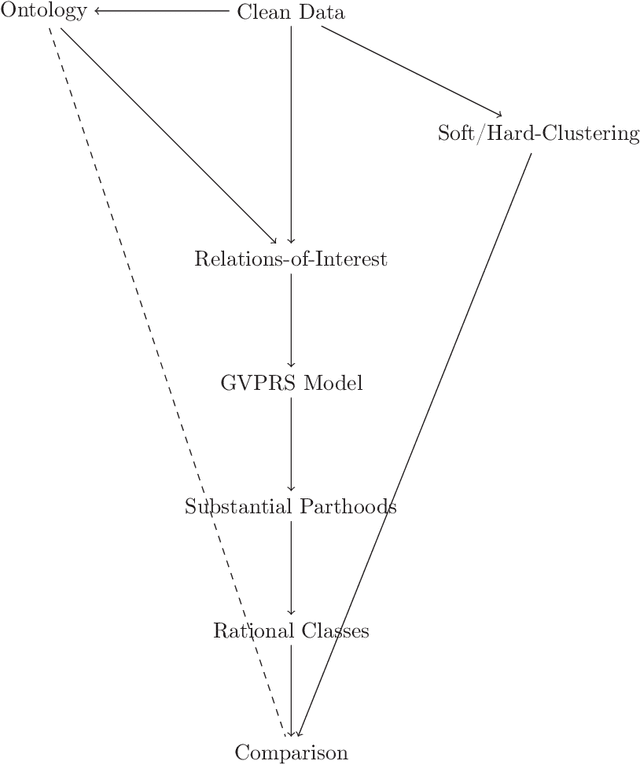
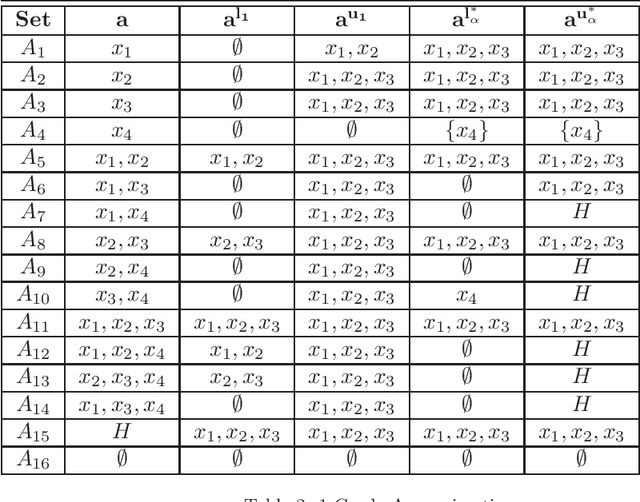
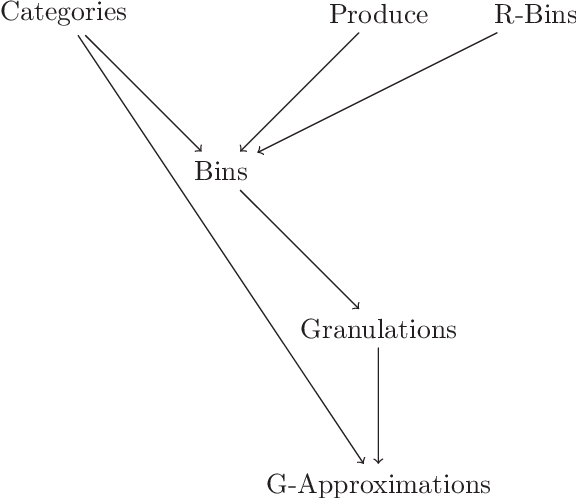
Rational approximations are introduced and studied in granular graded sets and generalizations thereof by the first author in recent research papers. The concept of rationality is determined by related ontologies and coherence between granularity, parthood perspective and approximations used in the context. In addition, a framework is introduced by her in the mentioned paper(s). Granular approximations constructed as per the procedures of VPRS are likely to be more rational than those constructed from a classical perspective under certain conditions. This may continue to hold for some generalizations of the former; however, a formal characterization of such conditions is not available in the previously published literature. In this research, theoretical aspects of the problem are critically examined, uniform generalizations of granular VPRS are introduced, new connections with granular graded rough sets are proved, appropriate concepts of substantial parthood are introduced, and their extent of compatibility with the framework is accessed. Furthermore, meta applications to cluster validation, image segmentation and dynamic sorting are invented. Basic assumptions made are explained, and additional examples are constructed for readability.