Sandor Radeleczki
Algebraic Approach to Directed Rough Sets
Apr 25, 2020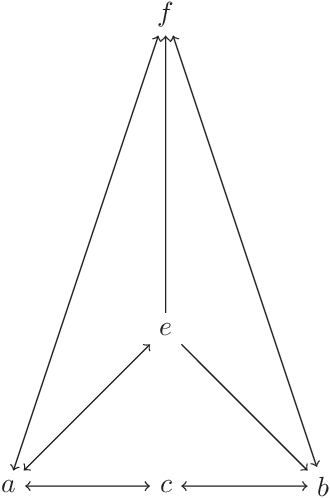
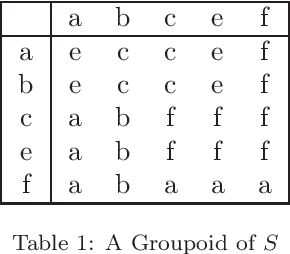
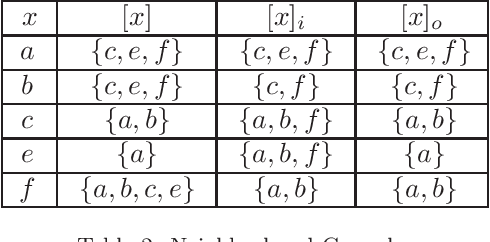
Abstract:In relational approach to general rough sets, ideas of directed relations are supplemented with additional conditions for multiple algebraic approaches in this research paper. The relations are also specialized to representations of general parthood that are upper-directed, reflexive and antisymmetric for a better behaved groupoidal semantics over the set of roughly equivalent objects by the first author. Another distinct algebraic semantics over the set of approximations, and a new knowledge interpretation are also invented in this research by her. Because of minimal conditions imposed on the relations, neighborhood granulations are used in the construction of all approximations (granular and pointwise). Necessary and sufficient conditions for the lattice of local upper approximations to be completely distributive are proved by the second author. These results are related to formal concept analysis. Applications to student centered learning and decision making are also outlined.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge